Основные методы решения задачи о собственных колебаниях пластинок

Известно, что аналитическими или точными методами можно решить лишь узкий круг частных задач, поэтому при решении рассматриваемой задачи широкое распространение получил целый ряд приближенных аналитических методов особенно вариационных, а так же численных.

1) Точный метод

Точное решение найдено для очень не многих случаев, в том числе для прямоугольной изотропной пластинки свободно опертой по контуру.

2) Вариационный метод

В основу вариационных методов положен принцип Релея, согласно которому собственные значения уравнения определяются по формуле:

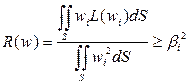
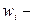любая допустимая функция для данной задачи, т.е. функция четырежды непрерывно дифференцируема, удовлетворяющая условиям граничным и полноты.

S – область ограниченная контуром пластины

при i=1 и условии, что: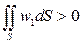

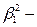является наименьшим собственным значением

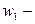соответствующее ему собств. функц.

Если ввести дополнительное условие:

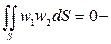условие ортогональности некоторой допустимой функции 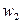функции 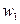, то формула 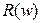будет определять следующее по величине собственное значение 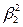, которое больше 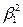, а 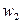будет соответствующей ему собственной функцией. В общем случае если известны i-1 низших собственных значений 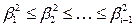и соотв. им ортогональная система функций 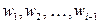, то формула 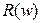будет определять высшее собственное значение. Если 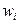– допустимая функция для которой выполняются условия обобщенной ортогональности низшим собственным функциям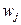

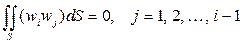
По энергетической форме

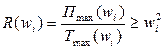
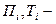пот. и кин. энергии деформации пластины соответственно

Для вычисления экстремумов в диф. уравнении широко используется метод Релея-Ридца.

Для решения этим методом необходимо задать форму колебаний в виде:

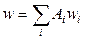
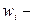допустимые функции задачи

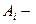произвольные постоянные должны обеспечивать получение минимальных значений 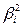. Условие минимума:

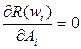
Условие приводят к системе уравнений. Эта система будет иметь не нулевое решение при условии, что её определитель равен нулю. Равенство определителя нулю дает частотное уравнение. На принципе Релея основывается вычислительный метод Бубнова-Галеркина. Форма колебаний задается в виде того же ряда, а для определения произвольных постоянных служит условие:

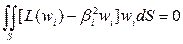
Условие нетривиальности этой системы приводит к частотному уравнению. Эти методы дают достаточно точные решения для низших частот колебаний. С повышением номера частоты точность падает.