Физическая нелинейность

При физической нелинейности

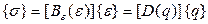
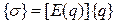
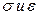– нелинейны.

Элементы 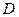определяют по форме

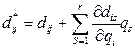
Тогда матрица жесткости:

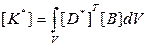
* - нелинейность

Тогда основное уравнение МКЭ станет нелинейным:

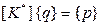
Решение этого уравнения может быть осуществлено в общем случае «явными» и «неявными» методами.

«Явные» и «неявные» методы.

В ANSYS поддерживаются неявные методы интегрирования уравнения динамики, использующие схему Ньюмарка. Расчет сводится к серии решений квазистатических задач с нагрузками, зависящими от времени. По сравнению с явными методами временные шаги относительно большие. Для высоко скоростных процессов, протекающих обычно в несколько миллисекунд и при очень больших деформациях приходится делать шаги весьма малыми, чтобы отследить изменение нагрузки и поведение конструкции. Инерционные нагрузки велики и определяются ускорениями конструкции. Для более точного их расчета эффективно вводить ускорения и скорости, число узловых степеней свободы и вычислять их на прямую, а не дважды дифференцируя перемещения, т.о. при малом шаге решение задач, может потребовать больше (10-ки – сотни раз) времени ЭВМ, чем при использовании явных методов, либо не сойтись.

Явными называют методы решения уравнений динамики не связанные с решением систем уравнений, но использующие рекуррентные соотношения, которые выражают перемещения, скорости и ускорения на данном шаге, через их значения на предшествующих шагах. Из-за очень малого размера шага явные методы применяются обычно только для расчета кратковременных процессов. Т.о. явные и неявные методы дополняют друг друга. Решатели ANSYS хорошо работают со статическими и квазистатическими задачами.

Явные решатели LS-DYNA из-за ошибок к тому времени мало эффективны для дин. и стат. задач. LS-DYNA использует спец. тех. помощник оптимизированный для решения высокоскоростных кратковременных процессов. Явный метод решения используемый в LS-DYNA обеспечивает наиболее эффективный расчет быстротекущих процессов, высокоскоростных процессов с большими динамическими, деформациями квазистатических задач с большими деформациями и высокой нелинейностью и так же сложных задач контакта. Решение основного уравнения неявными методами возможно при использовании итерационных методов. Рассмотрим 5 основных методов:

1) Метод последовательных приближений

На каждом шаге решения основного уравнения определяются через значения вектора q перемещения полученного на предыдущем шаге.

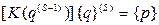
S – номер приближения (шаг)

Решение продлится до тех пор, пока разница результатов на данном и предыдущем шагах не будет достаточно малой. Метод обладает существенным недостатком. При сильной нелинейности он слабо сходится, а не редко расходится с точным решением, поэтому в таком виде применяется ограничено.

2) Метод упругих решений

Основан на выделении из матрицы жесткости K линейной и нелинейной составляющей:

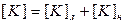
Тогда из основного уравнения с учетом этого получим:

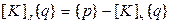
Методами последовательных приближений решаем уравнение:

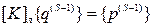
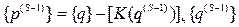
Процесс требует меньше операций, т.к. требует разового обращения к K_л, но сильно зависит от начального приближения и при большой разнице между линейным и нелинейным решениями могут расходиться или плохо сходиться.

3) Метод Ньютона-Равсела

Используется для ускорения сходимости. Пусть для приближенного S основного уравнения получено расхождение:

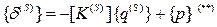
Зададим неизвестное перемещение 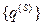, приращение 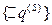, а затем погрешность для системы определяемой 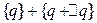на S+1, разложим в ряд Тейлора сохраняя первоначальные два члена:

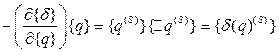- невязка(погрешность)

Внося это выражение в предыдущее и дифференцируя, получим:

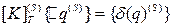
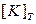- тангенциальная матрица, определенная на каждом шаге

Из последнего уравнения находим 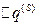, а затем уточняем решение:

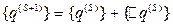
Число итераций уменьшается. Процесс обычно сходящийся, но не всегда. Рассмотренные три метода сводятся к ликвидации невязки.

4) Метод шагового погружения.

Основан на предположении, что в процессе нагружения отдельные составляющие внешней нагрузки изменяются пропорционально общему параметру нагружения.

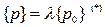
Дифференцируя основное уравнение МКЭ по 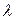и учитывая выражение 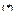мы получаем следующее выражение:

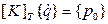
Недостаток: наличие «дрейфа» приближенного решения от точного. Накопленную невязку далее ликвидируют одним из первых трех методов.

5) Самокорректирующийся

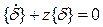
z – скалярный множитель

Используя это выражение и внося его в выражение для 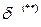, получим:

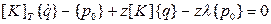
Решение последнего уравнения можно осуществить массовым методом в сочетании на каждом шаге с процедурой последовательных приближений. Этот метод сочетает достоинство всех методов. Сходимость итерационных методов сильно зависит от начальных приближений.