При вычислении N коэффициентов ДПФ согласно (8), или ОДПФ, согласно (11), надо выполнить N² достаточно трудоемких операций умножения. При больших массивах N (порядок 10³ и выше) использование (8) и (11) в реальном масштабе времени затруднительно из-за ограниченного быстродействия вычислительных устройств. Задача существенно упрощается с применением алгоритмов быстрого преобразования Фурье (БПФ), которые сводят обработку заданного массива данных к обработке массивов с меньшим числом членов и, тем самым, существенно уменьшается требуемое число операций умножения.
Сущность одного из алгоритмов БПФ для вычисления коэффициентов Ćn для массива вещественных данных {x(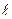 )}, объема N=2r, где r - целое число, состоит в следующем.
)}, объема N=2r, где r - целое число, состоит в следующем.
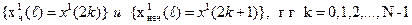 |
Разобьем исходный массив данных {x(
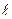 )} на две части с четными и нечетными номерами:
)} на две части с четными и нечетными номерами:
Согласно (8) коэффициенты N·Ćn на первом этапе разбиения равны:
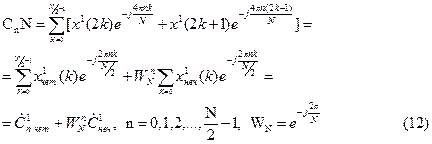 |
Из (12) следует, что последовательности коэффициентов Ć¹nчет и Ć¹nнеч обладают свойством периодичности с периодом N/2:
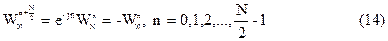 |
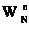
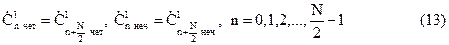 |
Кроме того, для n>N/2 множитель в (12) можно представить в виде:
 |
С учетом (12), (13) и (14) для всех n=0,1,2,3…N-1 можно записать:
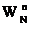 Причем знак "-" соответствует значениям n=N/2, N/2+1,… N-1. Подсчитаем, сколько требуется операций умножения при вычислении всех значений ĆnN по алгоритму (15). Для вычисления всех Ć¹nчет по (12) требуется (N/2)² умножений. Столько же умножения требуется для вычисления всех Ć¹nнеч. Кроме того, потребуется N умножений Ć¹nнеч на число +. Следовательно, потребуется 2(N/2)²+N умножений. При больших N требуемое число умножений равно N²/2=Nlog2N (при N=4), что в 2 раза меньше, чем по алгоритму (8).
Причем знак "-" соответствует значениям n=N/2, N/2+1,… N-1. Подсчитаем, сколько требуется операций умножения при вычислении всех значений ĆnN по алгоритму (15). Для вычисления всех Ć¹nчет по (12) требуется (N/2)² умножений. Столько же умножения требуется для вычисления всех Ć¹nнеч. Кроме того, потребуется N умножений Ć¹nнеч на число +. Следовательно, потребуется 2(N/2)²+N умножений. При больших N требуемое число умножений равно N²/2=Nlog2N (при N=4), что в 2 раза меньше, чем по алгоритму (8).
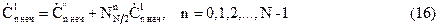 |
Четные отсчеты исходной последовательности Х¹чет(k) (их всего N/2) разобьем далее на втором этапе разбиения на четные и нечетные компоненты x"(2k) и x"(2k+1) (их число равно N/4). ДПФ последних обозначим Ć"nчет и Ć"nнеч. Тогда можно написать:
 Аналогичное разбиение выполняется над нечетными отсчетами исходной последовательности Х¹неч(k). Для вычисления всех ĆnN согласно формулам типа (16) (по массиву данных)
Аналогичное разбиение выполняется над нечетными отсчетами исходной последовательности Х¹неч(k). Для вычисления всех ĆnN согласно формулам типа (16) (по массиву данных)
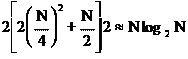 |
потребуется число умножений (при N=8).
Процесс разбиений можно продолжать r раз до тех пор, пока не получится последовательность из одного элемента, ДПФ которого совпадает с самим элементом. Далее надо собрать результаты отдельных разбиений для вычисления суммарных значений ĆnN. Анализ показывает, что число операций умножения, необходимых для вычисления БПФ, не больше, чем Nr=Nlog2N, что при больших N существенно меньше, чем N2. БПФ по рассматриваемому методу осуществляют в следующем порядке. Сначала для получения желательного при обработке сигнала порядке следования отсчетов x(k), k=0,1,2,…,N-1, выполняется двоично-инверсная перестановка исходной последовательности x(q), q=0,1,…, N-1. Для этого записывают порядковые номера элементов x(q) в двоичном коде и инвертируют порядок следования разрядов. Новый порядок следования элементов x(k) определяется номерами, получаемыми после инверсии разрядов.
Пример для N=4
| x(q) | x(k) | ||
| 0® | 00® | 00® | 0® |
| 1® | 01® | 10® | 2® |
| 2® | 10® | 01® | 1® |
| 3® | 11® | 11® | 3® |
Новый порядок следования элементов следующий: x(0), x(2), x(1), x(3). После этого поступают так: на первом этапе вычислений определяют 2-х точечные элементы ДПФ "новой" последовательности x(k), объединяя попарно элементы этой последовательности; на втором этапе из 2-х точечных ДПФ получают 4-х точечные ДПФ, пользуясь основной операцией данного метода (об этом ниже); затем 4-х точечные ДПФ объединяются в 8-ми точечные и т.д.
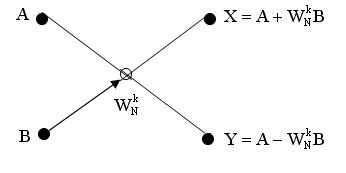
Базовые операции показывают, как два входных числа A и B объединяются для получения двух выходных чисел X и Y. Для метода прореживания во времени базовая операция имеет вид:
- в графическом виде
|
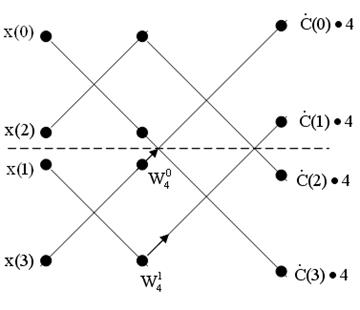
Граф для вычисления БПФ при N=4
или в форме уравнений
 |
При вычислении двухточечного ДПФ k=0 и выходные числа X и Y определяются без операции умножения X=A+B, Y=A-B.
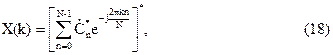 |
Чтобы воспользоваться рассмотренной процедурой БДПФ для вычисления ОДПФ, запишем (11) в виде
*) – комплексно-сопряженные числа.
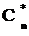 |
Вводя массив данных (вместо x(n)), можно найти сумму в (18) по изложенной выше методике БДПФ, а затем для нахождения x(k) найти комплексно-сопряженное значение полученного результата.
Существуют и другие методы вычисления БДПФ, т.е. другие методы группирования исходных данных x(k).
 2015-05-06
2015-05-06 790
790

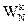 на B).
на B).







