Слайд 4,5,6

Величина средней квадратической (стандартной) ошибки простой случайной выборки:

1) повторный отбор: ;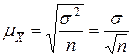

2) бесповторный отбор: .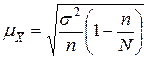

Т.е. величина ошибки зависит от колеблемости признака в генеральной совокупности и от объема выборки. Т.о. чем больше вариация тем больше ошибка, чем больше выборка тем меньше ошибка.

Величину 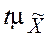называют предельной ошибкой выборки. Следовательно, предельная ошибка выборки 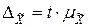, т.е. предельная ошибка равна t -кратному числу средних ошибок выборки.

t – критерий доверия, выбирается по таблице исходя из заданной вероятности.

Выборочное наблюдение проводится в целях распространения выводов полученных по данным выборки на генеральную совокупность.

Средняя арифметическая выборочной совокупности 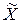, величина предельной ошибки выборочной 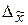(которая показывает, насколько будет отличаться выборочная средняя от генеральной в большую или в меньшую сторону). Получаем пределы, в которых с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называемые доверительными, а вероятность Р – доверительной вероятностью:

.

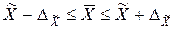Вероятность того, что величина генеральной средней выйдет за доверительные границы, будет равна 1 – Р, т.е. при Р = 0,9545 она будет равна 0,0455 или 0,01 при Р = 0,99. Событие, обладающее столь малой вероятностью, считается практически невозможным.