Рассматривается механическая система, описанная в Задании 1. Трение между призмой и опорной поверхностью отсутствует. Система приводится в движение из состояния покоя моментом 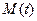 ,
,
приложенным к катку 1.
1. Используя общие теоремы динамики, составить систему
уравнений, описывающих движение заданной механической
системы. Исключая из этой системы уравнений внутренние
силы, получить дифференциальные уравнения, служащие для
определения зависимости 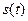 координаты точки
координаты точки 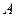 от времени
от времени
и 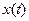 - закон движения призмы.
- закон движения призмы.
2. Получить дифференциальные уравнения движения
механической системы на основании общего уравнения динамики.
3. Получить дифференциальные уравнения движения
механической системы на основании уравнений Лагранжа 2-го рода.
4. Убедившись в совпадении результатов, полученных тремя
независимыми способами, проинтегрировать
дифференциальные уравнения движения системы, получив
зависимости 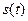 и
и 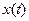 .
.
5. Построить графики зависимостей 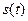 и
и 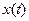 .
.
Варианты схем и зависимость вращающего момента от времени приведены в Таблице 2.
 2015-05-06
2015-05-06 482
482








