Пример 1.
Тело падает в сопротивляющейся среде с высоты 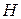 под действием силы тяжести
под действием силы тяжести 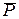 и силы сопротивления
и силы сопротивления 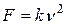 , пропорциональной квадрату скорости (
, пропорциональной квадрату скорости (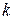 - постоянный коэффициент). С какой скоростью тело упадет на землю, если его начальная скорость
- постоянный коэффициент). С какой скоростью тело упадет на землю, если его начальная скорость 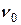 ?
?
Решение.
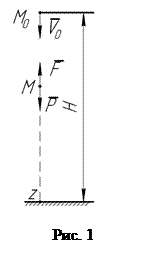
На схеме (рис. 1) показаны начальное (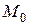 ) и текущее (
) и текущее (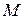 ) положение тела. Для начального положения тела показан вектор начальной скорости
) положение тела. Для начального положения тела показан вектор начальной скорости 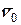 , для текущего – приложенные силы. Дифференциальное уравнение движения:
, для текущего – приложенные силы. Дифференциальное уравнение движения:
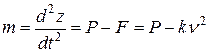 .
.
Так как
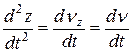 ,
,
то дифференциальное уравнение движения можно переписать в виде
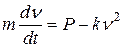 .
.
Но
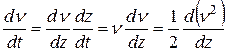 .
.
Поэтому:
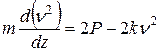 ;
;
или
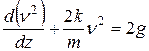 .
.
Это уравнение является линейным относительно 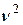 . Если обозначить
. Если обозначить 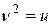 ,
, 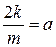 ,
, 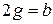 , его можно привести к виду
, его можно привести к виду
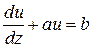 .
.
Общее решение этого уравнения:
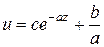 ,
,
где 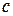 - произвольная постоянная.
- произвольная постоянная.
Возвращаясь к исходным обозначениям, имеем:
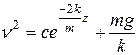 .
.
Начальное условие: при 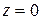 ,
, 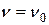 . Поэтому:
. Поэтому:
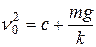 ,
, 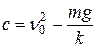 .
.
Следовательно:
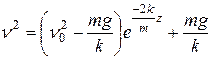 .
.
Следовательно, при 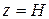 :
:
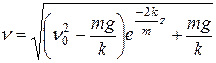 .
.
ПРИМЕР 2.
Лодка массой 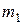 плавает в стоячей воде. На задней скамейке лодки, находящейся в покое, сидели два человека. Один из них, массой
плавает в стоячей воде. На задней скамейке лодки, находящейся в покое, сидели два человека. Один из них, массой 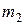 , перешел на нос лодки, пройдя по ней расстояние
, перешел на нос лодки, пройдя по ней расстояние 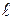 , другой, массой
, другой, массой 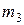 , переместился на среднюю скамейку на расстояние
, переместился на среднюю скамейку на расстояние 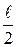 . На какое расстояние переместится при этом лодка?
. На какое расстояние переместится при этом лодка?
При решении задачи людей считать материальными точками, сопротивлением воды пренебречь.
Решение.
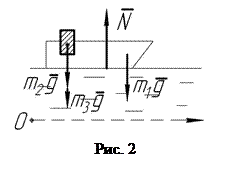 На схеме (рис. 2) показаны внешние силы, действующие на механическую систему, состоящую из лодки и двух материальных точек, схематизирующих пассажиров лодки: силы тяжести
На схеме (рис. 2) показаны внешние силы, действующие на механическую систему, состоящую из лодки и двух материальных точек, схематизирующих пассажиров лодки: силы тяжести  ,
, 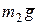 ,
, 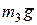 и выталкивающая сила воды
и выталкивающая сила воды 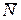 . Все внешние силы направлены по вертикали, их проекции на неподвижную горизонтальную ось Ох равны нулю. Поэтому дифференциальное уравнение движения центра масс С системы в проекциях на ось Ох будет:
. Все внешние силы направлены по вертикали, их проекции на неподвижную горизонтальную ось Ох равны нулю. Поэтому дифференциальное уравнение движения центра масс С системы в проекциях на ось Ох будет:
 ,
,
или 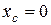 . Отсюда, интегрируя, находим
. Отсюда, интегрируя, находим 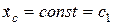 . Значение постоянной интегрирования определяется из начального условия: при
. Значение постоянной интегрирования определяется из начального условия: при 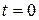
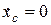 (так как вся система в начальный момент неподвижна). Тогда
(так как вся система в начальный момент неподвижна). Тогда 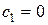 и
и 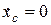 . Интегрируя еще раз, получаем
. Интегрируя еще раз, получаем 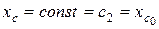 (
(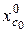 - координата центра масс системы при
- координата центра масс системы при 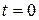 ).
).
По определению координата центра масс механической системы определяется выражением:
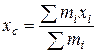 .
.
Поэтому из равенства 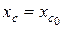 следует
следует 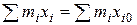 или
или 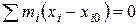 , или окончательно
, или окончательно 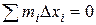 , где
, где 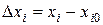 есть приращение координаты центра тяжести
есть приращение координаты центра тяжести 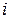 -го тела, входящего в систему, или, что то же, проекция его перемещения на ось Х.
-го тела, входящего в систему, или, что то же, проекция его перемещения на ось Х.
В нашем случае абсолютные перемещения пассажиров 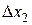 и
и 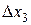 складываются из переносного перемещения вместе с лодкой
складываются из переносного перемещения вместе с лодкой 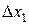 и относительных по отношению лодки:
и относительных по отношению лодки:
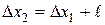 ,
, 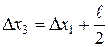 .
.
Поэтому:
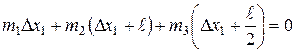 .
.
Отсюда:
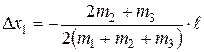 .
.
Знак минус означает, что лодка перемещается против Х.
ПРИМЕР 3.
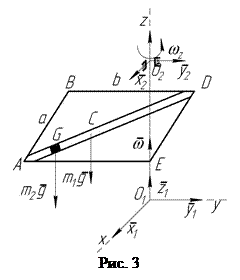 Горизонтальная прямоугольная пластина АВДЕ со сторонами АВ=а= 0,30 м, ВД = b =0,40 м и массой
Горизонтальная прямоугольная пластина АВДЕ со сторонами АВ=а= 0,30 м, ВД = b =0,40 м и массой 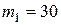 кг может вращаться без трения вокруг неподвижной вертикальной оси
кг может вращаться без трения вокруг неподвижной вертикальной оси 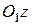 , проходящей через точку Е (рис. 3). На пластине имеется прямоугольный желоб АД, по которому может двигаться без трения груз массой
, проходящей через точку Е (рис. 3). На пластине имеется прямоугольный желоб АД, по которому может двигаться без трения груз массой 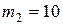 кг.
кг.
В начальный момент пластина и груз неподвижны, и груз находится в точке А, затем груз начинает двигаться по пластине под действием внутренних сил по закону 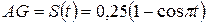 , м.
, м.
Определить угловую скорость 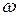 пластины как функцию времени и найти ее значение в момент, когда груз окажется в точке Д.
пластины как функцию времени и найти ее значение в момент, когда груз окажется в точке Д.
Решение.
На схеме показаны внешние силы, действующие на систему пластина – груз: силы тяжести  ,
, 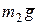 и реакции
и реакции 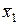 ,
, 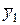 ,
, 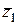 ,
, 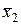 ,
, 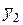 подшипника
подшипника 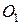 и подшипника
и подшипника 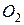 . Моменты каждой из этих сил относительно оси
. Моменты каждой из этих сил относительно оси 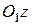 равны нулю. Поэтому по теореме об изменении кинетического момента
равны нулю. Поэтому по теореме об изменении кинетического момента 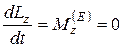 . Отсюда
. Отсюда 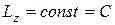 . Постоянная интегрирования
. Постоянная интегрирования 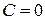 , так как в начальный момент система неподвижна. Следовательно
, так как в начальный момент система неподвижна. Следовательно 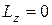 .
.
Так как система состоит из двух тел – пластины и груза, то ее кинетический момент равен сумме кинетического момента пластины 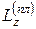 и момента количества движения
и момента количества движения 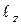 груза:
груза: 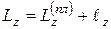 . Пластина вращается вокруг неподвижной оси, поэтому
. Пластина вращается вокруг неподвижной оси, поэтому 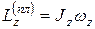 (
(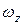 - проекция вектора угловой скорости
- проекция вектора угловой скорости 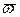 на ось
на ось 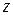 ).
).
Момент инерции пластины по теореме Штейнера:
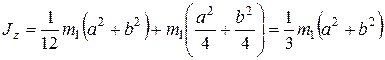 .
.
При определении момента количества движения груза учитываем, что его движение сложное и абсолютная скорость 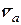 равна геометрической сумме переносной
равна геометрической сумме переносной 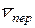 и относительной
и относительной 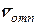 скоростей.
скоростей.
По теореме Вариньона момент вектора относительно оси равен алгебраической сумме моментов его составляющих, поэтому момент количества движения груза равен сумме моментов векторов 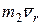 и
и  :
:
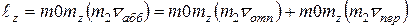 .
.
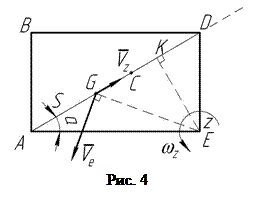 На рис. 4 вектор относительной скорости
На рис. 4 вектор относительной скорости 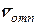 направлен в положительную сторону оси
направлен в положительную сторону оси 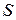 , что соответствует случаю, когда:
, что соответствует случаю, когда:
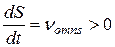 .
.
В этом случае 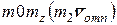 отрицателен (точка движется по отношению к оси
отрицателен (точка движется по отношению к оси 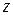 по часовой стрелке). Если будет
по часовой стрелке). Если будет 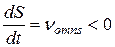 (проекция
(проекция 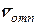 на ось
на ось 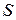 отрицательно), то направление
отрицательно), то направление 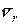 будет противоположным и
будет противоположным и 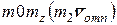 должен быть положительным. В обоих случаях справедливо равенство
должен быть положительным. В обоих случаях справедливо равенство
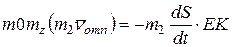 .
.
Аналогично направление вращения пластины и переносной скорости 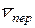 показаны на рис. 4 для случая, когда
показаны на рис. 4 для случая, когда 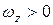 . В этом случае
. В этом случае 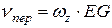 и
и 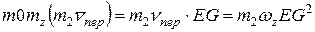 . Если же будет
. Если же будет 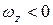 , то вектор
, то вектор 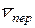 будет направлен в противоположную сторону и равен по модулю
будет направлен в противоположную сторону и равен по модулю 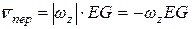 ; момент количества движения будет равен:
; момент количества движения будет равен:
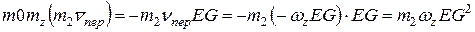 .
.
Таким образом, и для момента вектора 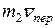 в обоих случаях (
в обоих случаях (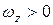 и
и 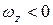 ) получили одинаковое выражение
) получили одинаковое выражение 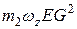 . Следовательно, при любых знаках величин
. Следовательно, при любых знаках величин 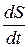 и
и 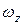 момент количества движения груза:
момент количества движения груза:
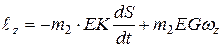 .
.
Вычислим 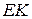 и
и 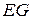 . Из
. Из 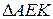
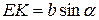 . Из
. Из 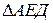
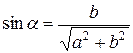 . Следовательно,
. Следовательно, 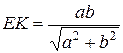 . Из
. Из 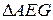 по теореме косинусов
по теореме косинусов 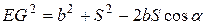 . Из
. Из 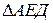
 . Поэтому
. Поэтому 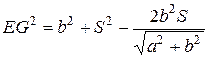 .
.
Подставляя 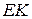 и
и 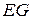 в выражение для
в выражение для 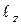 и прибавив к нему кинетический момент пластины, получим выражение для кинетического момента системы, который по доказанному ранее равен нулю:
и прибавив к нему кинетический момент пластины, получим выражение для кинетического момента системы, который по доказанному ранее равен нулю:
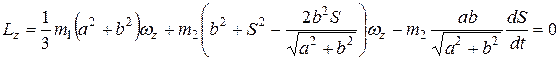 .
.
После подстановки числовых значений получаем:
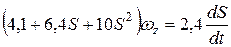 ,
,
откуда
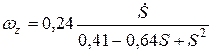 ,
,
или
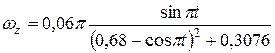 .
.
Чтобы определить значение 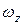 в момент прихода груза в точку
в момент прихода груза в точку 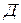 , замечаем, что в этот момент
, замечаем, что в этот момент 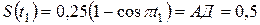 , или
, или 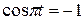 ; откуда
; откуда 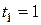 с. При
с. При 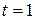 с получаем
с получаем 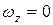 .
.
ПРИМЕР 4.
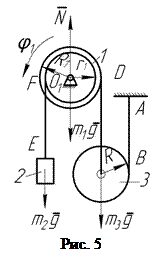
Ступенчатый шкив 1, имеющий массу 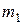 и радиус инерции относительно оси вращения
и радиус инерции относительно оси вращения 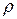 , обмотан гибкими нерастяжимыми нитями. К нити, сходящей со ступени радиуса
, обмотан гибкими нерастяжимыми нитями. К нити, сходящей со ступени радиуса 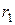 прикреплен груз 2 массы
прикреплен груз 2 массы 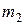 . К нити, сходящей со ступени радиуса
. К нити, сходящей со ступени радиуса 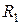 , шарнирно прикреплен цилиндр 3 в точке
, шарнирно прикреплен цилиндр 3 в точке 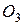 , лежащей на его оси. Этот цилиндр также обмотан нитью, конец которой закреплен в точке А. Участки
, лежащей на его оси. Этот цилиндр также обмотан нитью, конец которой закреплен в точке А. Участки 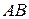 и
и 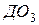 параллельны. Радиус цилиндра равен
параллельны. Радиус цилиндра равен 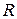 , а его масса -
, а его масса - 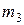 и равномерно распределена по его объему. Массы и радиусы удовлетворяют условию
и равномерно распределена по его объему. Массы и радиусы удовлетворяют условию 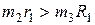 . Пренебрегая трением в шарнирах, определить угловую скорость
. Пренебрегая трением в шарнирах, определить угловую скорость 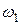 ступенчатого шкива в функции угла
ступенчатого шкива в функции угла 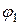 его поворота, его угловое ускорение
его поворота, его угловое ускорение 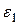 , натяжения нитей
, натяжения нитей 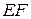 ,
, 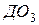 ,
, 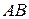 и реакцию оси
и реакцию оси 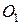 . В начальный момент система неподвижна.
. В начальный момент система неподвижна.
Решение.
Кинетическая энергия ступенчатого вала, вращающегося вокруг неподвижной оси:
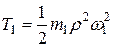 .
.
Кинетическая энергия груза 2, совершающего поступательное движение:
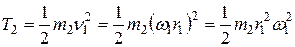 .
.
Кинетическая энергия цилиндра, совершающего плоскопараллельное движение:
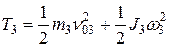 .
.
Мгновенный центр скоростей сечения цилиндра плоскостью чертежа находится в точке В (так как скорость участка нити АВ равна нулю).
Поэтому 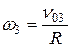 . Момент инерции цилиндра
. Момент инерции цилиндра 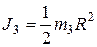 . Подставив эти выражения в формулу для
. Подставив эти выражения в формулу для 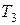 , получим:
, получим:
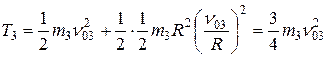 .
.
Учитывая, что 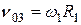 , окончательно
, окончательно
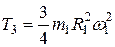 .
.
Кинетическая энергия системы
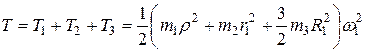 .
.
При повороте ступенчатого шкива на угол 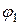 груз
груз 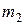 опускается на величину
опускается на величину 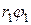 , а ось цилиндра поднимается на
, а ось цилиндра поднимается на 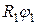 . Сумма работ сил тяжести:
. Сумма работ сил тяжести:
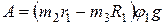 .
.
Другие силы, приложенные в данной системе, работы не совершают.
Так как в начальный момент система неподвижна, то по теореме об изменении кинетической энергии:
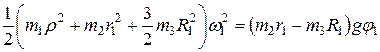 .
.
Это равенство и определяет зависимость 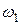 от
от 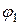 .
.
Чтобы найти угловое ускорение шкива 1, дифференцируем левую и правую части этого равенства по времени:
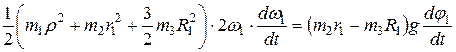 .
.
Так как 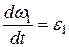 ,
, 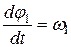 , то отсюда получаем:
, то отсюда получаем:
 .
.
 Чтобы определить натяжение
Чтобы определить натяжение 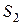 нити
нити 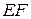 , напишем уравнение второго закона Ньютона для груза 2, к которому приложены силы
, напишем уравнение второго закона Ньютона для груза 2, к которому приложены силы 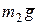 и
и 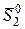 (рис. 6):
(рис. 6):
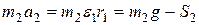 ,
,
где  - ускорение груза.
- ускорение груза.
Отсюда
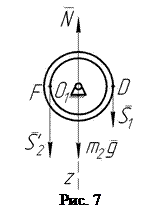
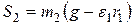 .
.
Для определения натяжения 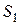 нити
нити 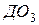 применим к ступенчатому шкиву дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. К шкиву приложены силы
применим к ступенчатому шкиву дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. К шкиву приложены силы  ,
, 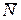 ,
, 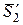 ,
, 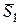 (рис. 7). Поэтому
(рис. 7). Поэтому
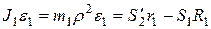 .
.
Так как 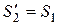 , то отсюда
, то отсюда
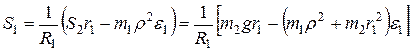 .
.
Для определения реакции 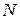 применим к шкиву теорему о движении центра масс:
применим к шкиву теорему о движении центра масс:
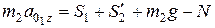 .
.
Так как 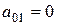 , то
, то
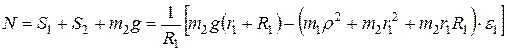 .
.
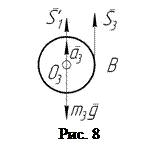
Наконец, для определения натяжения 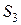 нити АВ применим теорему о движении центра масс к цилиндру 3, на который действуют внешние силы
нити АВ применим теорему о движении центра масс к цилиндру 3, на который действуют внешние силы 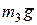 ,
, 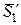 ,
, 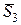 (рис. 8):
(рис. 8):
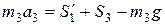 .
.
Так как 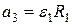 , то отсюда
, то отсюда
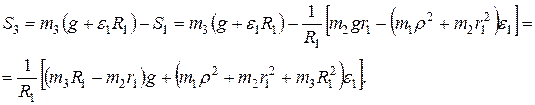
Подставив сюда выражение 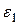 , получим
, получим 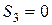 .
.
ПРИМЕР 5.
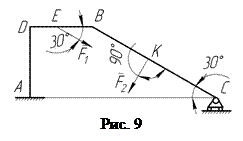 Пользуясь принципом возможных перемещений, определить для составной конструкции, изображенной на схеме (рис. 9), реактивный момент и вертикальную составляющую реакции заделки, если
Пользуясь принципом возможных перемещений, определить для составной конструкции, изображенной на схеме (рис. 9), реактивный момент и вертикальную составляющую реакции заделки, если 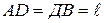 .
. 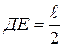 ,
, 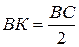 ,
, 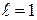 м,
м, 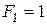 кН,
кН, 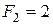 кН.
кН.
Решение.
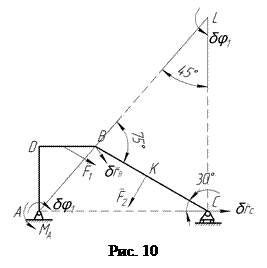
Для определения реактивного момента 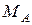 заменим заделку в точке А шарнирно-неподвижной опорой, компенсировав отброшенную связь ее реакцией – реактивной парой сил с неизвестным моментом
заменим заделку в точке А шарнирно-неподвижной опорой, компенсировав отброшенную связь ее реакцией – реактивной парой сил с неизвестным моментом 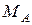 (рис. 10).
(рис. 10).
Получившейся механической системе с одной степенью свободы даем возможное перемещение, повернув мысленно уголок АДВ на бесконечно малый угол 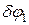 , например по часовой стрелке. Точка В получит при этом возможное перемещение
, например по часовой стрелке. Точка В получит при этом возможное перемещение 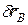 , направленное перпендикулярно АВ и равное по модулю
, направленное перпендикулярно АВ и равное по модулю 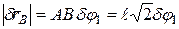 ; точка С получит возможное перемещение
; точка С получит возможное перемещение 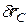 , параллельное опорной плоскости шарнирно-неподвижной опоры С; стержень ВС повернется вокруг точки L – центра поворота, определенного как и МЦС в кинематике, как точка пересечения перпендикуляров, проведенных через точки В и С к направлениям их возможных перемещений. Угол
, параллельное опорной плоскости шарнирно-неподвижной опоры С; стержень ВС повернется вокруг точки L – центра поворота, определенного как и МЦС в кинематике, как точка пересечения перпендикуляров, проведенных через точки В и С к направлениям их возможных перемещений. Угол 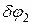 , на который стержень ВС повернется вокруг точки L, определяется равенством:
, на который стержень ВС повернется вокруг точки L, определяется равенством:
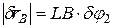 , откуда
, откуда
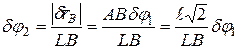 .
.
Для нахождения 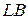 воспользуемся теоремой синусов. Из
воспользуемся теоремой синусов. Из 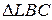 (см. рис. 10):
(см. рис. 10):
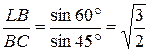 .
.
Отсюда:
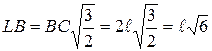 .
.
Следовательно,
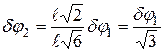 .
.
Теперь подсчитаем и приравняем к нулю сумму работ сил 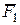 ,
, 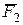 и пары с моментом
и пары с моментом 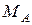 при возможном перемещении системы.
при возможном перемещении системы.
Используя правило: работа сил, приложенных к вращающемуся телу, равна взятому с соответствующим знаком произведению момента сил относительно оси вращения на угол поворота. Поэтому:
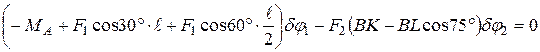 .
.
 Здесь в первых скобах записана сумма моментов силы
Здесь в первых скобах записана сумма моментов силы 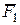 и реактивной пары относительно точки А. Для определения момента силы
и реактивной пары относительно точки А. Для определения момента силы 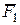 она была разложена на вертикальную и горизонтальную составляющие. Со знаком плюс записаны моменты, направленные в сторону поворота
она была разложена на вертикальную и горизонтальную составляющие. Со знаком плюс записаны моменты, направленные в сторону поворота 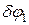 . Момент пары записан со знаком минус, так как она стремится вращать уголок в направлении, противоположном возможному перемещению
. Момент пары записан со знаком минус, так как она стремится вращать уголок в направлении, противоположном возможному перемещению 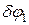 . Во вторых скобках записано плечо силы
. Во вторых скобках записано плечо силы 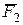 относительно точки L. Знак минус перед второй скобкой поставлен потому, что сила
относительно точки L. Знак минус перед второй скобкой поставлен потому, что сила 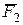 стремится вращать стержень ВС вокруг точки L в направлении противоположном возможному перемещению
стремится вращать стержень ВС вокруг точки L в направлении противоположном возможному перемещению 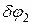 .
.
Заменяя в предыдущем равенстве 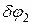 его выражением через
его выражением через 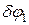 и учитывая, что
и учитывая, что 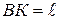 ,
, 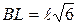 , можем переписать его в виде:
, можем переписать его в виде:
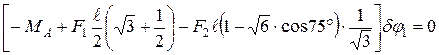 .
.
Так как 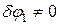 , то отсюда:
, то отсюда:
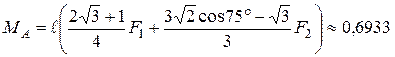 кН×м.
кН×м.
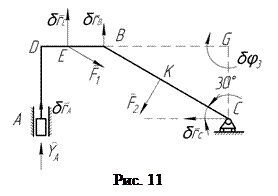
Для нахождения вертикальной составляющей реакции заделки А заменим в исходной схеме заделку ползуном, который может перемещаться в вертикальном направлении и к которому жестко прикреплен угол АДВ, а отброшенную связь компенсируем вертикальной реакцией 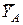 (рис. 11).
(рис. 11).
Даем получившейся механической системе возможное перемещение, мысленно переместив угол АДВ поступательно вверх (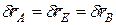 ). Стержень ВС повернется вокруг центра поворота G на угол
). Стержень ВС повернется вокруг центра поворота G на угол 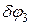 . Уравнение принципа возможных перемещений запишется в виде:
. Уравнение принципа возможных перемещений запишется в виде:
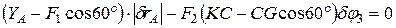 ,
,
откуда, учитывая, что 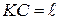 ,
, 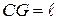 ,
, 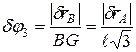 , получаем
, получаем
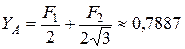 кН.
кН.
ПРИМЕР 6.
Сплошной однородный цилиндр 1 массой 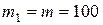 кг и радиусом
кг и радиусом 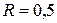 м может вращаться без трения вокруг неподвижной горизонтальной оси
м может вращаться без трения вокруг неподвижной горизонтальной оси 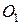 . С цилиндром жестко скреплены тонкие однородны стержни 3 и 4 массой
. С цилиндром жестко скреплены тонкие однородны стержни 3 и 4 массой 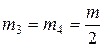 и длиной
и длиной 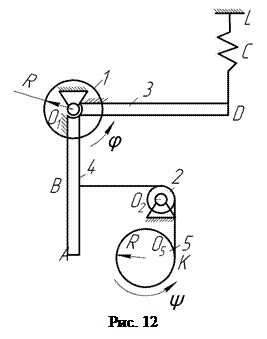
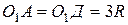 каждый. В середине В стержня 4 к нему прикреплена нить, перекинутая через невесомый блок 2 и намотанная на цилиндр 5, одинаковый с цилиндром 1. При движение системы ось
каждый. В середине В стержня 4 к нему прикреплена нить, перекинутая через невесомый блок 2 и намотанная на цилиндр 5, одинаковый с цилиндром 1. При движение системы ось 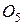 цилиндра 5 перемещается по вертикали. В точке Д к стержню 3 прикреплена пружина жесткостью
цилиндра 5 перемещается по вертикали. В точке Д к стержню 3 прикреплена пружина жесткостью 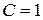 кН/м. В начальном положении системы стержень 3 и участок нити между стержнем и блоком расположены горизонтально, а стержень 4 и ось пружины – вертикально; пружина растянута на величину
кН/м. В начальном положении системы стержень 3 и участок нити между стержнем и блоком расположены горизонтально, а стержень 4 и ось пружины – вертикально; пружина растянута на величину 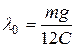 .
.
Начальные значения обобщенных координат 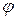 и
и 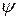 равны нулю, а обобщенных скоростей -
равны нулю, а обобщенных скоростей - 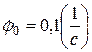 ,
, 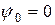 . Трением в осях
. Трением в осях 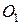 ,
, 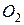 , массой пружины и нити пренебрегаем.
, массой пружины и нити пренебрегаем.
Используя уравнение Лагранжа II рода, найти кинематические уравнения движения системы при малых отклонениях цилиндра 1 от начального положения и определить круговую частоту и период колебания системы.
Решение.
Кинетическая энергия системы равна сумме кинетических энергий вращающегося цилиндра 1 с жестко присоединенными к нему стержнями и цилиндра 5, совершающего плоскопараллельное движение:
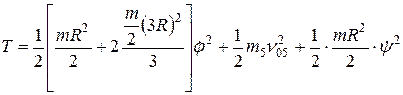 .
.
В этом выражении 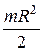 - момент инерции цилиндра относительно его оси;
- момент инерции цилиндра относительно его оси; 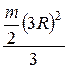 - момент инерции стержня; в квадратных скобках – момент инерции цилиндра 1 с жестко присоединенными к нему стержнями.
- момент инерции стержня; в квадратных скобках – момент инерции цилиндра 1 с жестко присоединенными к нему стержнями.
Скорость 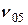 центра цилиндра 5 равна сумме скорости точки
центра цилиндра 5 равна сумме скорости точки 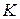 нити и скорости
нити и скорости 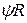 точки
точки 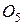 во вращательном движении вокруг полюса
во вращательном движении вокруг полюса 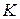 .
.
 Для определения
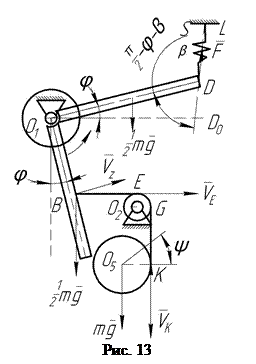
Для определения 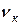 рассмотрим положение системы, при котором цилиндр 1 и стержни 3 и 4 отклонены от начального положения на угол
рассмотрим положение системы, при котором цилиндр 1 и стержни 3 и 4 отклонены от начального положения на угол 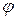 (рис. 13). Скорость точки
(рис. 13). Скорость точки 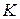 нити равна скорости точки Е, в которой участок нити ВЕ касается блока 2. Так как нить нерастяжима, то проекция скоростей точек В и Е на направление нити равны. Поэтому:
нити равна скорости точки Е, в которой участок нити ВЕ касается блока 2. Так как нить нерастяжима, то проекция скоростей точек В и Е на направление нити равны. Поэтому:
 .
.
Теперь воспользуемся малостью отклонений стержней от начального положения. Как известно, функция 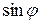 и
и 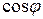 можно разложить в ряды Маклорена:
можно разложить в ряды Маклорена:
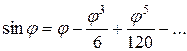 ;
;
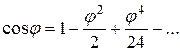 .
.
При «малых» 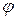 (до 0,1 радиана) значения
(до 0,1 радиана) значения 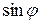 и
и 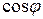 отличаются от первых членов соответствующих разложений менее чем на 0,5%. Поэтому можно принять
отличаются от первых членов соответствующих разложений менее чем на 0,5%. Поэтому можно принять 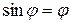 ,
, 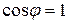 . Так как при «малом»
. Так как при «малом» 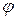 угол
угол 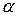 также является «малым», то
также является «малым», то 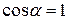 . Поэтому в этом случае
. Поэтому в этом случае
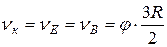 , тогда
, тогда 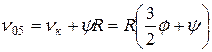 .
.
Подставляя 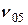 в ранее написанное выражение для Т, после простых преобразований приводим его к виду:
в ранее написанное выражение для Т, после простых преобразований приводим его к виду:
 .
.
Для нахождения обобщенных сил 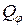 и
и 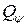 , соответствующих обобщенным координатам
, соответствующих обобщенным координатам 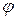 и
и 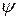 , вновь обратимся к рис. 13. Чтобы определить
, вновь обратимся к рис. 13. Чтобы определить 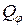 , дадим мысленно системе возможное перемещение, при котором обобщенная координата
, дадим мысленно системе возможное перемещение, при котором обобщенная координата 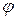 изменяется на бесконечно малую величину
изменяется на бесконечно малую величину 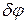 , а обобщенная координата
, а обобщенная координата 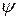 не изменяется. В этом случае точка В получит возможное перемещение
не изменяется. В этом случае точка В получит возможное перемещение 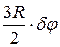 , направленное по вектору
, направленное по вектору 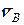 . Такие же по абсолютному значению перемещения при «малых»
. Такие же по абсолютному значению перемещения при «малых» 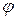 получат точки Е, G, К и
получат точки Е, G, К и 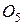 . Поэтому сила тяжести цилиндра 5 совершит работу
. Поэтому сила тяжести цилиндра 5 совершит работу 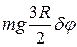 . Работа сил тяжести стержней и силы упругости
. Работа сил тяжести стержней и силы упругости 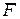 пружины равна произведению их момента относительно оси вращения
пружины равна произведению их момента относительно оси вращения 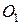 на угол поворота
на угол поворота 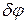 , т.е.
, т.е.
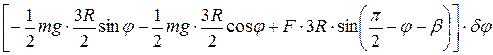 .
.
Из рис. 13 видно (см. 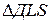 ), что
), что
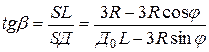 .
.
При 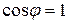
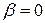 . Этот результат означает, что угол
. Этот результат означает, что угол 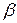 является малым более высокого порядка, чем
является малым более высокого порядка, чем 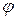 (имеет порядок квадрата
(имеет порядок квадрата 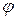 ), и по сравнению с
), и по сравнению с 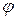 им можно пренебречь. Тогда сумма работ всех задаваемых сил при повороте цилиндра 1 на угол
им можно пренебречь. Тогда сумма работ всех задаваемых сил при повороте цилиндра 1 на угол 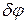 будет:
будет:
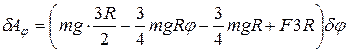 .
.
Укорочение пружины, соответствующее положению цилиндра 1, повернутому из начального положения на угол 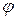 , равно разности
, равно разности 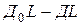 . Длина
. Длина 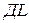 укоротившейся пружины равна
укоротившейся пружины равна
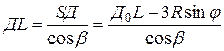 ,
,
или при «малых» 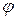 :
:
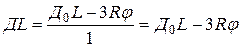 .
.
Следовательно, укорочение пружины
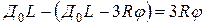 .
.
Так как в начальный момент пружина была растянута на величину 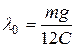 , то ее растяжение уменьшается и станет
, то ее растяжение уменьшается и станет 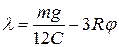 , а упругая сила будет
, а упругая сила будет 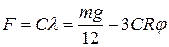 .
.
Обобщенна сила, соответствующая углу 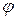 :
:
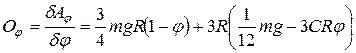 ,
,
или окончательно
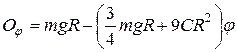 .
.
Для нахождения обобщенной силы 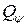 , соответствующей обобщенной координате
, соответствующей обобщенной координате 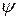 , нужно сообщить системе возможное перемещение, при котором
, нужно сообщить системе возможное перемещение, при котором 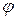 останется неизменным, а
останется неизменным, а 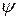 увеличивается на бесконечно малую величину
увеличивается на бесконечно малую величину 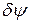 . В этом случае работу совершает только сила тяжести цилиндра 5:
. В этом случае работу совершает только сила тяжести цилиндра 5: 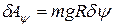 .
.
Обобщенная сила:
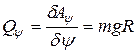 .
.
Теперь составим уравнение Лагранжа:
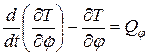 ,
, 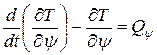 .
.
Частные производные:
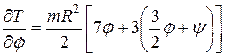 ;
; 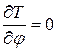 .
.
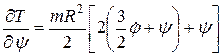 ,
, 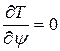 .
.
Уравнение Лагранжа будет иметь вид:
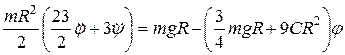 ;
;
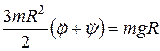 .
.
Из второго уравнения после сокращения его на  :
:
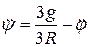 .
.
Подставив это выражение в первое уравнение, после простых преобразований получим:
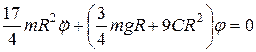 .
.
Обозначим:
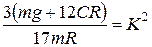 .
.
Величина:
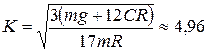 1/с
1/с
и представляет искомую круговую частоту колебаний.
Период колебаний:
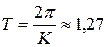 с.
с.
Общее решение дифференциального уравнения малых колебаний цилиндра:
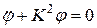
есть функция:
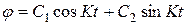 .
.
Для нахождения постоянных интегрирования 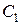 и
и 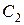 используем начальные условия: при
используем начальные условия: при 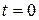 ,
, 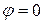 ,
, 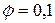 (1/с).
(1/с).
Из первого условия следует 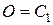 ; из второго условия, учитывая, что:
; из второго условия, учитывая, что:
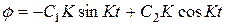 ,
,
получаем 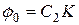 ;
; 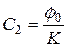 . Поэтому окончательно:
. Поэтому окончательно:
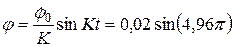 .
.
Для нахождения 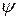 интегрируем ранее полученное уравнение:
интегрируем ранее полученное уравнение:
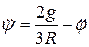 .
.
Имеем:
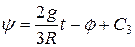 .
.
Из начальных условий: при 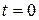 ,
, 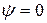 ,
, 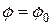 следует
следует 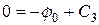 ;
; 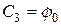 . Тогда:
. Тогда:
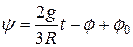 .
.
Интегрируя еще раз, получаем:
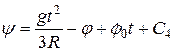 .
.
Из начальных условий: при 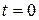 ,
, 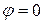 ,
, 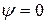 следует
следует 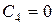 . Поэтому:
. Поэтому:
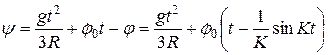 .
.
После подстановки числовых значений:
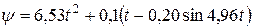 .
.
ПРИМЕР 7.
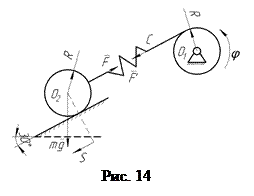 Вывести кинематические уравнения движения системы, показанной на рис. 14, пренебрегая массой пружины. Качение катка происходит без проскальзывания. Трением в оси
Вывести кинематические уравнения движения системы, показанной на рис. 14, пренебрегая массой пружины. Качение катка происходит без проскальзывания. Трением в оси  пренебречь. Блок и каток – одинаковые цилиндры радиусом
пренебречь. Блок и каток – одинаковые цилиндры радиусом 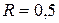 м и массой
м и массой 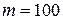 кг, равномерно распределенной по их объему. Жесткость пружины
кг, равномерно распределенной по их объему. Жесткость пружины 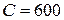 Н/м.
Н/м.
Начальные значения обобщенных координат 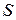 и
и 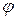 равны нулю; начальное удлинение пружины
равны нулю; начальное удлинение пружины 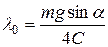 ; начальные значения обобщенных скоростей
; начальные значения обобщенных скоростей 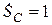 м/с,
м/с, 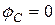 .
.
Решение.
Кинетическая энергия системы:
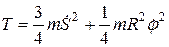 .
.
Обобщенные силы:
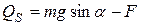 ,
, 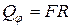 ,
,
где 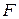 - сила упругости пружины.
- сила упругости пружины.
Уравнение Лагранжа для рассмотренной системы:
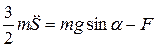 ;
; 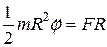 .
.
Сила упругости 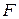 зависит от деформации
зависит от деформации 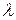 пружины, которая равна
пружины, которая равна 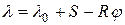 , где
, где 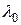 - начальное значение деформации. Обозначим
- начальное значение деформации. Обозначим 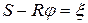 . Тогда
. Тогда 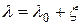 ;
; 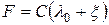 . С другой стороны, дифференциальные уравнения движения системы можно представить в виде:
. С другой стороны, дифференциальные уравнения движения системы можно представить в виде:
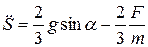 ;
; 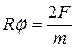 .
.
Вычитая из первого уравнение второе, получаем
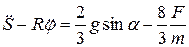 ,
,
или
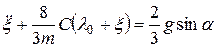 .
.
Подставляя заданное значение 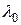 , получим:
, получим:
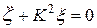 , где
, где 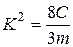 .
.
Решением этого дифференциального уравнения при начальных условиях: при 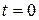 ,
, 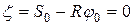 ,
, 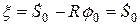 является функция:
является функция: 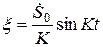 . Тогда
. Тогда 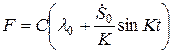 .
.
Дифференциальные уравнения движения системы принимают вид:
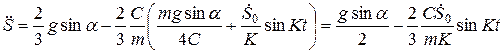 ;
;
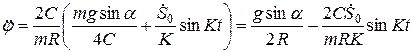 .
.
Интегрируя эти уравнения при начальных условиях: 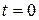 ,
, 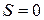 ,
, 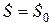 ,
, 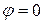 ,
, 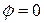 , получим:
, получим:
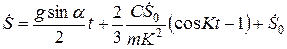 ;
;
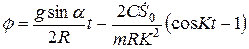 ;
;
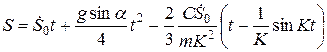 ;
;
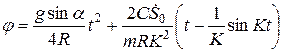 .
.
После подстановки численных значений получим:
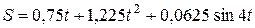 ;
;
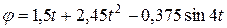 .
.
 2015-05-06
2015-05-06 1333
1333








