2015-05-06
386
1. Равномерное распределение: для такой случайной величины плотность вероятности является постоянной, т.е.
 |
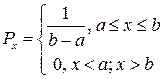
Функция распределения вероятности такой случайной величины на интервале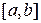 
линейно возрастает от 0 до 1:
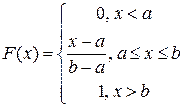
Математическое ожидание:
;
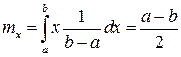Дисперсия: согласно (3.6) с учётом математического ожидания получаем:
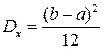
СКО: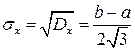 
.
2. Нормативный закон распределения – достаточно часто встречается на практике, например, он характерен для помех канала связи: при этом одномерная плотность вероятности нормальной случайной величины определяется как:
,
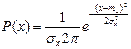где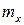 
и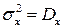 
– соответственно мат ожидание и дисперсия процесса (случайные величины).
График плотности вероятности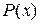 
в этом случае имеет вид (для 
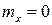и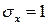 
):
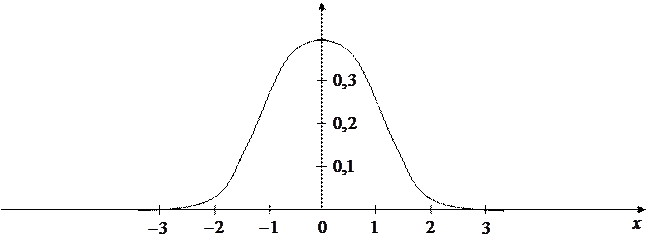
Функция распределения вероятности в этом случае обычно выражается через интеграл вероятности:
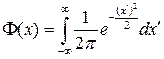
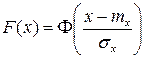
В зарубежной литературе часто используется функция ошибок (error function):
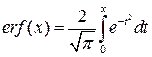
между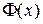 
и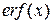 
существует взаимосвязь:
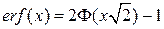
С учётом этого функция распределения для нормального закона с математическим ожиданием 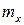и дисперсией 
:
.
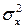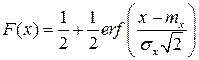Важное свойство:
При суммировании достаточно большого числа равномощных статистических независимых случайных величин с произвольными плотностями распределения вероятности, плотность распределения вероятности суммы стремиться к нормальной. Это положение носит название центральной предельной теоремы.
Кроме того, для математического анализа случайных величин полезным является то, что из некоррелированности гауссовых случайных величин следует их статистическая независимость.
