2015-05-06
482
Для описания СМО используется обозначение <×|×|×> (×).
Первое место в этом обозначении характеризует входной поток, а именно, характеризует распределение вероятностей промежутков поступлений между соседними клиентами.
Второе место является характеристикой обслуживающих приборов, а именно, характеризует распределение вероятностей времени обслуживания.
Третье место характеризует число обслуживающих приборов.
Четвертое место характеризует дисциплину очереди.
В основном мы будем изучать системы, когда в качестве распределения, стоящих на первом и втором местах, будет использоваться показательное распределение. Это связано с тем, что такие СМО адекватно описываются процессами гибели и размножения, которые мы изучали выше. И, такие системы будут обозначаться следующим образом:
< M | M | m > (очередь длины N) или < Ml | Mm | m > (очередь длины N).
Рассмотрим подробно некоторые известные системы.
1. Система < M | M |1> (с очередью)
Предположим, что X (t) – число клиентов в системе в момент t, и интенсивность поступления и обслуживания клиентов не меняется, т.е. lk =l, k = 0, 1,... mk = m, k = 1, 2,... Диаграмма выглядит так:
|
|
|
 |
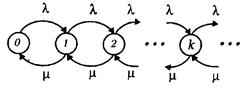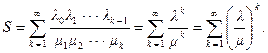Cоставляем систему дифференциальных уравнений для нахождения вероятности P k (t) = P(X (t) = k). Для этого исследуем сходимость ряда
 |
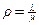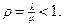Обозначим.
 |
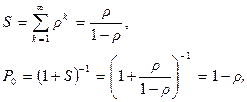Если r < 1, то S < ¥ и стационарный режим существует. Если же r ³ 1, то S = ¥. Таким образом в данной системе стационарный режим существует тогда и только тогда, когда
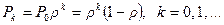В условиях существования стационарного режима найдем:
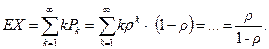среднее число клиентов в системе:
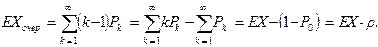среднее число клиентов в очереди:
Еще одной важной характеристикой системы является q – время ожидания начала обслуживания в стационарном режиме.
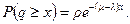Лемма 1. Если r < 1, то вероятность того, что P(q ³ x) равна
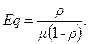Т.е. прежде чем начнут обслуживать, придется ждать как минимум x единиц времени. Отсюда можно получить (проверьте самостоятельно) с реднее время ожидания начала обслуживания, или среднее время, проведенное в очереди:
Величина E q является важной характеристикой «качества» обслуживания»: чем меньше E q, тем обслуживание лучше.
Обозначим через E v – среднее время, проведенное в системе:
 |
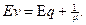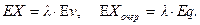Тогда
2. Система < M | M | m > (с очередью)
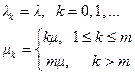Пусть X (t) – число клиентов в системе в момент t. Предположим, что
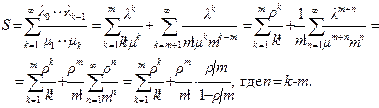Найдем условие стационарности. Для этого исследуем сходимость ряда S.
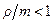Если, то S < ¥ и стационарный режим существует. Таким образом в данной системе стационарный режим существует тогда и только тогда, когда r < m.
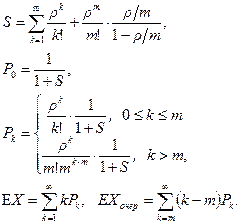В условиях существования стационарного режима
|
|
|
Предположим, что q – время, проведенное в очереди.
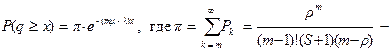Лемма 2. При r < m вероятность того, что P(q ³ x) равна
- вероятность того, что все приборы заняты.
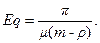Тогда среднее время, проведенное в очереди (проверьте самостоятельно)
3. Система < M | M |¥>
Это система, когда любому вновь прибывшему клиенту находят прибор.
Предположим, что lk = l, k = 0, 1, ¼; mk = km, k = 1, 2, ¼ Диаграмма выглядит так:
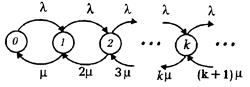
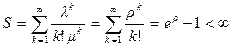Найдем условие стационарности.
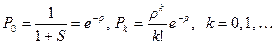Т.е. независимо от того, какой r, стационарный режим существует всегда. Отсюда,
Для системы <М│М│∞> можно вывести формулы:(самостоятельно)
.
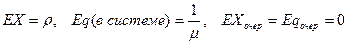Также можно привести формулы для оценки P k(t) и в случае, когда процесс еще не достиг стационарного режима.
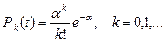, где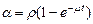 
.
Как видно, и для неустановившегося режима X (t) подчиняется пуассоновскому распределению. Очевидно, что EX (t) = α.
