2015-05-06
641
1) 
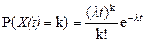X(t) есть пуассоновский процесс с параметромλ, т.е.
2) Приращение пуассоновского процесса однородное.
Обозначим через X (( a,b ]) = X ( b ) – X ( a ) приращение процесса, которое может быть интерпретировано как число клиентов, поступающих в систему в промежутке ( a,b ]. Однородность означает выполнение условия:
P( X (( a,b ]) = k) = P( X ((0, b - a ]) = k) = P( X ( b - a ) = k),
т.е. распределение вероятностей числа клиентов, поступающих в систему в промежутке ( a,b ], зависит только от длины этого промежутка.
3) Приращения пуассоновского процесса независимы.
Рассмотрим промежуток (0, b ] и предположим, что он разбит на непересекающиеся промежутки (0, b 1], ( b 1, b 2], ¼, ( b N-1, b N]. Пусть b 0 = 0. Тогда X (( b 0, b 1]), X (( b 1, b 2]), ¼, X (( b N-1, b N]) – число клиентов, поступающих в систему в соответствующие периоды времени. Эти величины независимы, т.е.
P( X (( b 0, b 1]) = i 1, ¼, X (( b N-1, b N]) = i N) =
= P( X (( b 0, b 1]) = i 1) ××× P( X (( b N-1, b N]) = i N).
Доказательства этих свойств можно найти в [ ].
§ 
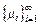
3. Процесс гибели и размножения
Построим процесс гибели и размножения X ( t ) «конструктивно».
|
|
|
Рассмотрим две последовательности и. Первая - отвечает за поступление клиентов в систему (размножение), а вторая - за обслуживание клиентов (гибель):
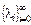- интенсивность поступления клиентов (число клиентов, которое поступает в систему за единицу времени, если в ней i клиентов).
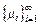- интенсивность обслуживания клиентов (число клиентов, которое обслуживается в системе за единицу времени, если в ней i клиентов).
Кроме того, пусть заданы две независимые последовательности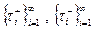 
независимых случайных величин с показательным распределением с параметром 
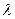=1.
Процесс X (t) строится так. Пусть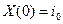 
, где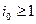 
. Тогда на интервале 
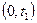процесс X (t) сохранит свое значение 
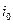, где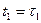 
,
.
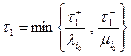В момент t 1 значение процесса X ( t ) либо увеличится, либо уменьшится на единицу в соответствии с тем, какой из двух моментов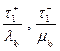 
наступит раньше:
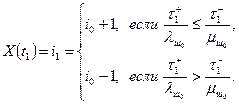
Мы положили, таким образом, значение процесса X (t) в точке t 1 равным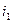 
; тогда эволюция процесса X ( t ) на интервале 
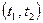, где 
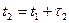и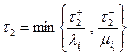 
, подчиняется тому же закону закону: X ( t ) не меняется на этом интервале в момент t 2
увеличивается на единицу, если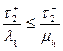 
, и уменьшается на единицу в противном случае.
Если же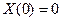 
, то значение процесса X ( t ) увеличивается на единицу в случайный момент 
.
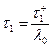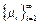
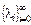Построенный таким образом процесс 
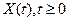, называется однородным по времени процессом гибели и размножения; его распределения полностью определяются набором параметров, и начальным распределением X(0):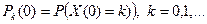 
Удобно использовать следующую диаграмму для представления развития процесса X (t):
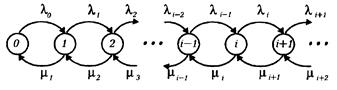
Стрелочки сверху соответствуют динамике процесса размножения: из i-го состояния процесс переходит в (i+1)-е состояние с интенсивностью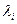 
; стрелочки снизу соответсвуют динамике процесса гибели: с интенсивностью 
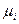процесс из i-го состояния переходит в (i-1)-е состояние.
|
|
|
Набор функций
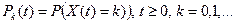
описывает распределение процесса X(t); ниже мы приведем систему уравнений, которым удовлетворяют эти функции.
Отметим, что не всякому набору параметров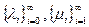 
отвечает «невырожденный» процесс X(t); дело в том, что если числа 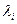растут очень быстро при 
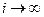, то процесс X(t) в конечный момент t может «взорваться», т.е. с положительной вероятностью превысить любой уровень и возрасти до 
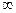. Так ведут себя, например, популяция бактерий в благоприятной среде. Аналогично устроены процессы, описывающие химические реакции, приводящие к взрыву.
Процессы X(t), для которых все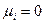 
, относятся к так называемым процессам чистого размножения. Процессы, для которых 
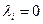, называют процессами чистой гибели.
Следующая лемма дает необходимые и достаточные условия на параметры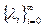 
, которые гарантируют конечность процесса чистого размножения 
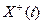с параметрами .
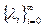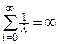Лемма. Пусть 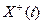процесс чистого размножения с параметрами 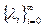. Тогда для конечности процесса 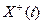необходимо и достаточно, чтобы расходился ряд
Пусть X(t) процесс гибели и размножения с теми же параметрами 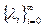процесса 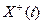, а также параметрами 
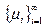. Очевидно, что
P(X(t) < ¥) ³ P(X+(t) < ¥).
Поэтому из леммы получаем следствие.
Следствие. Если для произвольного процесса гибели размножения X(t) выполнено условие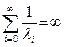 
, то для любого 
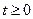справедливо P( X(t) < ¥) = 1, т.е. процесс конечен.
Доказательство леммы можно найти в [ ].
