Дифференциальные уравнения, отвечающие процессу гибели и размножения

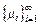
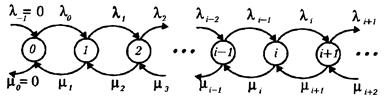
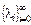Предположим, что X (t) – процесс гибели и размножения с характеристиками и. Пусть для некоторых конечных чисел A и B имеют место неравенства l_i £ A + Bi, i = 0, 1,...Это условие гарантирует конечность процесса X (t). При этом мы условимся, что в каждое состояние приходит верхняя стрелочка слева (даже в состояние 0), при этом интенсивность рождения λ может равняться нулю (например, λ_–1= = 0); из каждого состояния выходит нижняя стрелочка влево, и интенсивность гибели μ тоже может равняться нулю (например, λ_–1 = 0). Доопределение таким образом диаграммы не меняет суть дела, однако в дальнейших рассуждениях будет полезно. Рассмотрим диаграмму, отвечающую нашему процессу X (t):

Обозначим, как и ранее, через

P_k (t) = P (Х (t) = k), k = 0,1,…,

вероятности того, что в фиксированный момент t число клиентов X (t) будет равно k.

Теорема 1. Характеристики 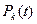процессаX(t), определенное выше, удовлетворяет следующей системе дифференциальных уравнений

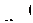
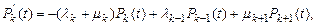
где k = 0,1,…, и начальным условиям

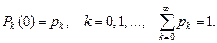
Нелишне пояснить, что первая строка (при k = 0) системы уравнений (1) имеет вид

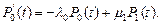
Доказательство. Обозначим через P _k(t + Δ) = P (X (t + Δ) = k).

Воспользуемся определением производной функции одной переменной:

.

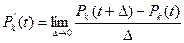Рассмотрим такие события:

A ₀(t, Δ) = {на отрезке [ t, t +Δ] процесс X (t) не совершил ни одного скачка};

A ₁(t, Δ) = {на отрезке [ t, t +Δ] процесс X (t) совершил ровно один скачок};

A ₂(t, Δ) = {на отрезке [ t, t +Δ] процесс X (t) совершил два скачка и более}.