|
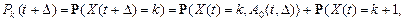
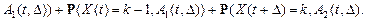
Обозначим далее через 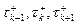 три показательные случайные величины с параметрами
три показательные случайные величины с параметрами 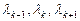 ; через
; через 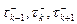 три показательные случайные величины с параметрами
три показательные случайные величины с параметрами 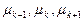 . Пусть все эти величины независимы. Тогда верно
. Пусть все эти величины независимы. Тогда верно
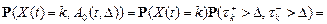
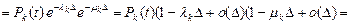
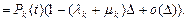
В последнем равенстве мы воспользовались следующим свойством показательной функции: e –Δ = 1 – Δ + o (Δ) при Δ → 0.
Аналогично получаем
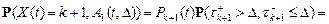
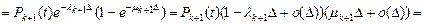
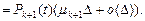
Точно также устанавливается соотношение
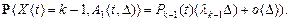
Пусть 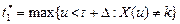 – момент последнего перед t +Δ скачка процесса Х (t);
– момент последнего перед t +Δ скачка процесса Х (t); 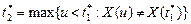 – момент предпоследнего перед t +Δ скачка процесса X (t).
– момент предпоследнего перед t +Δ скачка процесса X (t).
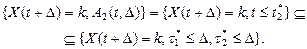 Обозначим еще
Обозначим еще 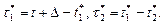 Тогда очевидно, что
Тогда очевидно, что
Это событие заключается в том, что происходят ровно два скачка.
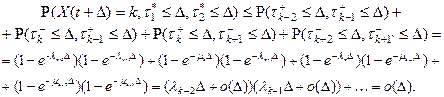 Осталось заметить, что
Осталось заметить, что
Т.е вероятность того, что в системе будет два и более скачка равна нулю.
Подставляя в (2) полученные соотношения, приходим к следующему равенству:
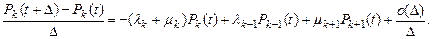
Переходя в последнем равенстве к пределу при Δ → 0, получаем уравнение (1). Теорема доказана.
Рассмотрим систему дифференциальных уравнений:
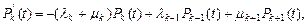
если существуют пределы:
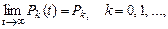
удовлетворяющие условию
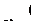
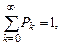
то вероятности Рk называются стационарными вероятностями (характеристиками), а относительно системы говорят, что она находится в стационарном (установившемся) режиме. Стационарные вероятности удовлетворяют следующей системе алгебраических уравнений:
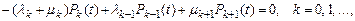 (4)
(4)
Система (4) получается, если приравнять нулю левую часть системы (1). Решая последовательно систему (4), можно выразить числа Рk через Р0:
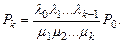
Подставляя в соотношение (3) получаем:
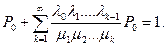
Очевидно далее, что сходимость ряда
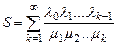
есть условие существования стационарного режима в системах массового обслуживания. В этом случае стационарные характеристики Рk процесса X(t) находятся с помощью формул
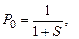
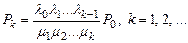
 2015-05-06
2015-05-06 296
296








