Вращение твердого тела вокруг неподвижной оси

В этом случае движение твердого тела определяется уравнением

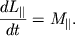
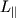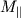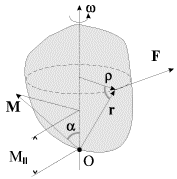
Здесь - это момент импульса относительно оси вращения, то есть проекция на ось момента импульса, определенного относительно некоторой точки, принадлежащей оси. - это момент внешних сил относительно оси вращения, то есть проекция на ось результирующего момента внешних сил, определенного относительно некоторой точки, принадлежащей оси, причем выбор этой точки на оси, как и в случае с 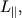значения не имеет. Действительно (рис. 3.4), 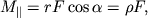где 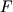- составляющая силы, приложенной к твердому телу, перпендикулярная оси вращения, 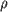- плечо силы 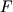относительно оси.

Рис. 3.4.

Поскольку 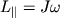( 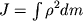- момент инерции тела относительно оси вращения), то вместо 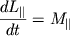можно записать

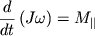
(3.8)

или

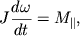
(3.9)

поскольку в случае твердого тела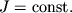

Уравнение (3.9) и есть основное уравнение динамики вращательного движения твердого тела вокруг неподвижной оси. Его векторная. форма имеет вид:

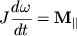
(3.10)

Вектор 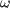всегда направлен вдоль оси вращения, а 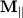- это составляющая вектора момента силы вдоль оси.

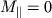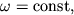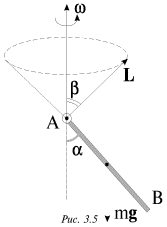
В случае получаем соответственно и момент импульса относительно оси 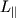сохраняется. При этом сам вектор L, определенный относительно какой-либо точки на оси вращения, может меняться. Пример такого движения показан на рис. 3.5.

Рис. 3.5.

Стержень АВ, шарнирно закрепленный в точке А, вращается по инерции вокруг вертикальной оси таким образом, что угол 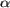между осью и стержнем остается постоянным. Вектор момента импульса L, относительно точки А движется по конический поверхности с углом полураствора 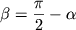однако проекция L на вертикальную ось остается постоянной, поскольку момент силы тяжести относительно этой оси равен нулю.