Рассмотрим движение точки под действием трех сил: одна восстанавливающая сила, вторая - сила демпфирования (сила вязкого сопротивления), а третья зависит от времени. 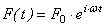 - гармоническая возмущающая сила.
- гармоническая возмущающая сила.
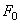 - амплитуда возмущающей силы.
- амплитуда возмущающей силы.
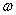 - круговая частота возмущающей силы.
- круговая частота возмущающей силы.
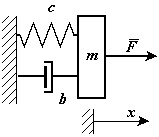
Рис.40
Дифференциальное уравнение движения точки с массой m, закрепленной на упругом элементе и демпфере (рис.40), под действием возмущающей гармонической силы имеет вид:
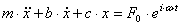
Задавая решение уравнения в виде: 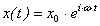 и подставляя его в дифференциальное уравнение получим алгебраическое уравнение для определения амплитуды вынужденных колебаний.
и подставляя его в дифференциальное уравнение получим алгебраическое уравнение для определения амплитуды вынужденных колебаний.
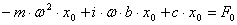 .
.
Разделим его на массу и обозначим 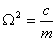 ,
, 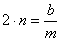 , тогда
, тогда 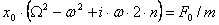 и окончательно
и окончательно
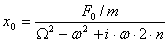 - амплитуда вынужденных колебаний.
- амплитуда вынужденных колебаний.
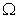 - частота собственных колебаний
- частота собственных колебаний
Материальная точка колеблется с амплитудой 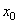 и частотой возмущающей силы
и частотой возмущающей силы 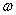 .
.
Построим зависимость модуля амплитуды 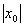 от частоты возмущающей силы
от частоты возмущающей силы 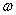 (рис.41).
(рис.41).
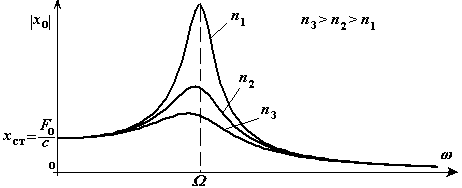
Рис.41
Модуль амплитуды вынужденных колебаний возрастает от 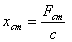 (при
(при 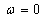 ) до некоторой величины, а затем убывает до нуля (при
) до некоторой величины, а затем убывает до нуля (при 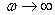 ).
).
 2015-05-06
2015-05-06 1079
1079








