Сформулировать и доказать теорему о главном моменте количеств движения механической системы. Сформулировать теорему Резаля

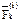- Механическая система N материальных точек. К k-ой точке системы (k = 1, 2,..., N) приложены равнодействующие внешних и внутренних сил.

ДУ движения: 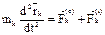или 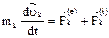(1). Учтём, что масса постоянна и помножим (1) векторно слева на 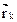: 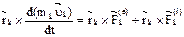(2). Преобразуем (2), используя тождество: 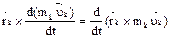и просуммируем по k: 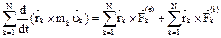. Геометрическая сумма моментов внутренних сил относительно любого центра равна нулю, а сумма производных, равна производной от суммы: 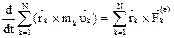или 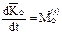: производная по времени от главного момента количества движения механической системы относительно неподвижного центра О равна главного моменту всех действующих на систему внешних сил, относительно того же центра.

- При движении механической системы скорость конца вектора главного момента количества движения системы относительно некоторого неподвижного центра О равна главному моменту всех действующих на систему вешних сил относительно того же центра.