Тема: Интегрирование дифференциальных уравнений движения материальной точки».
Исходные данные:
Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течение τ сек. Его начальная скорость υА. Коэффициент трения скольжения тела по плоскости равен f.
В точке В тело покидает плоскость и попадает в точку С плоскости наклоненной под углом β к горизонту, находясь в воздухе Т сек.
При решении задачи тело принять за материальную точку; сопротивление воздуха не учитывать.
Исходные данные:
Α=150, υА=2м/с; f =0,2; h=4 м; B=450
Схема показана на рисунке 1.
Определить параметры движения точки на участках АВ и ВС (скорость в точке В - υb,время движения на участке ВС - T, длину участка АВ - l, скорость в точке С - υc, расстояние, пройденное телом по оси ОХ на участке ВС - d, время в течении которого точка движется на участке АВ - τ) и уравнение траектории точки на участке ВС.
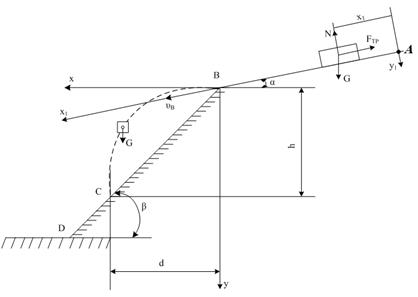
Рис. 1
Рассмотрим движение тела на участке АВ. Принимая тело за материальную точку, покажем действующие на него силы: вес 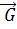 , нормальную реакцию
, нормальную реакцию 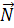 и силу трения скольжения
и силу трения скольжения 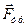 .
.
Составим дифференциальное уравнение движения тела на участке АВ в проекции на ось x1:
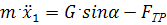 ,
,
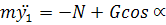 , т.к. движение вдоль оси y1 отсутствует, то
, т.к. движение вдоль оси y1 отсутствует, то 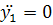 ;
;
Отсюда: 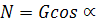 .
.
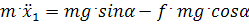
Разделив на m, получим:
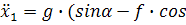 α);
α);
Дважды интегрируя дифференциальное уравнение, получаем:
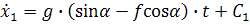
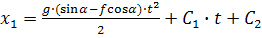
Для определения постоянных интегрирования, воспользуемся начальными условиями задачи: при 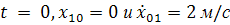 . Подставив начальные условия в уравнения получим:
. Подставив начальные условия в уравнения получим:
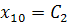 ;
; 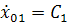
Найдем постоянные:
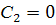 ;
; 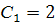 м/с
м/с
Тогда:
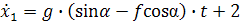
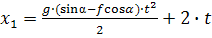
Подставим конечные условия: 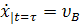 ;
; 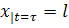 .
.
Получим уравнения:
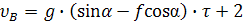
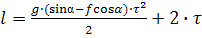
Рассмотрим движение тела на участке ВС.
Показав силу тяжести 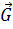 , действующую на камень, составим дифференциальные уравнения его движения в проекциях на координатные оси
, действующую на камень, составим дифференциальные уравнения его движения в проекциях на координатные оси 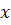 и
и 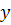 :
:
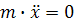 ;
;
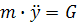 =mg;
=mg;
Разделив на m, получим:

Интегрируем дифференциальное уравнение дважды:
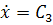 ;
;
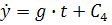 ;
;
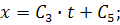
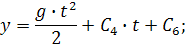
Начальные условия при t = 0:
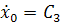 =
= 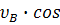 α;
α;
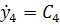 =
= 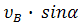 ;
;
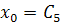 =0;
=0;
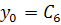 =0;
=0;
Получим следующие уравнения проекций скорости тела:
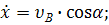
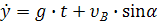
и уравнения его движения
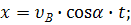
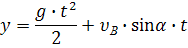
Подставим конечные условия. В момент падения, 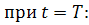
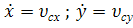 ;
;
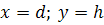 .
.
Получим систему уравнений:
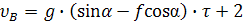 (1)
(1)
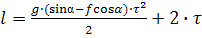 (2)
(2)
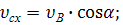 (3)
(3)
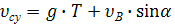 (4)
(4)
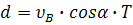 (5)
(5)
 (6)
(6)
Определим d:
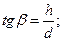 т.к.
т.к. 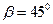 , то h=d
, то h=d
Используя уравнения движения камня, найдем время Т движения тела от точки В до точки С и скорость 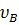 в точке В. Из уравнения (5):
в точке В. Из уравнения (5):
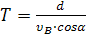 ; Подставив в уравнение (6), получим:
; Подставив в уравнение (6), получим:
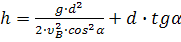 ; Решим совместно уравнения (5) и (6):
; Решим совместно уравнения (5) и (6):
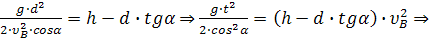 Отсюда:
Отсюда:
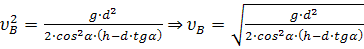
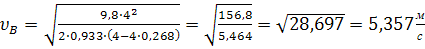 ; Определив скорость
; Определив скорость 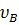 найдем время падения T на участке ВС:
найдем время падения T на участке ВС:
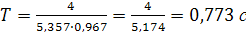
Определив 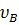 , найдем из уравнений (1) и (2)время
, найдем из уравнений (1) и (2)время 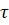 движения тела от точки А до точки В на участке АВ и длину
движения тела от точки А до точки В на участке АВ и длину 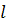 участка АВ:
участка АВ:
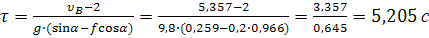
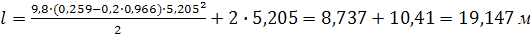
Скорость камня при падении найдем через проекции скорости на оси координат:
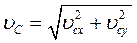
Для момента t = Т = 0,773 сек.
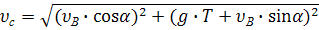
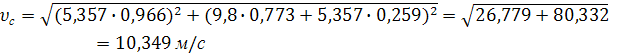
Уравнение траектории движения тела на участке ВС найдем, исключив параметр t из уравнений движения, получим уравнение параболы:
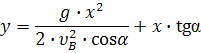
Подставив значения, получим:
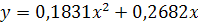
Таблица ответов:
| d, м | 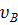 , м/с , м/с
| Т, с | 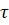 , с , с
| 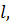 м м
| 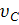 , м/с , м/с
| у=у(t) |
| 5,357 | 0,733 | 5,205 | 19,147 | 10,349 | У=0,18x2+0.2682x |
 2015-05-06
2015-05-06 2407
2407








