Правило варьирования не отличаются от правил дифференцирования
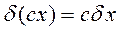
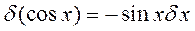
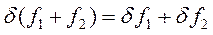 и т.д.
и т.д.
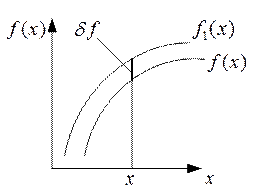
Рис.43
7.4 Перемещения возможные и действительные.
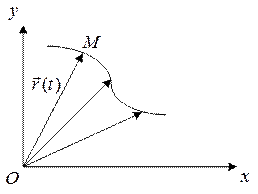
Рис.44
Действительные перемещения это перемещения, происходящие в пространстве и во времени, т.е. действительным перемещением точки называется бесконечно малое перемещение под действием внешних сил в соответствии с законом движения и уравнением связи, происходящие по траекториям при постоянном изменении времени.
Если рассматриваем действительные перемещения бесконечно малые, то они являются дифференциалом, т.к. меняется аргумент время и за счет этого меняется функция  .
.
Возможные перемещения не происходят на самом деле, но они могут происходить, так как допускаются связями.
Определение: возможным перемещением называется любое бесконечно малое, воображаемое перемещение, допускаемое в данный момент связями.
Время (аргумент) фиксированное (остановленное) поэтому возможное перемещение является вариацией  .
.
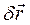 - изменение вида функции при постоянном аргументе.
- изменение вида функции при постоянном аргументе.
Классический пример: кривошипно-ползунный механизм:
Рис. 45
точка 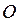 - нет возможных перемещений;
- нет возможных перемещений;
точка 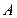 - возможно движение по окружности в обе стороны;
- возможно движение по окружности в обе стороны;
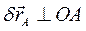
Перемещения в одну и в другую сторону считаются как одно.
Перемещение 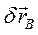 - возможное перемещение точки
- возможное перемещение точки 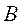 .
.
Перемещение 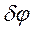 - возможен поворот стержня
- возможен поворот стержня  вокруг точки
вокруг точки 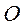 .
.
Перемещение 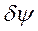 - возможен поворот шатуна
- возможен поворот шатуна  вокруг мгновенного центра скоростей стержня
вокруг мгновенного центра скоростей стержня  .
.
7.5 Виртуальная работа.
а) Виртуальная работа силы.
Определение: Виртуальной работой силы, приложенной к какой-либо точке тела, движущегося поступательно, называется скалярное произведение вектора силы на вектор возможного перемещения точки, в которой приложена эта сила:
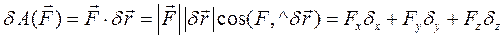 (203)
(203)
Как уже говорилось работа это число положительное, отрицательное или ноль.
Знак зависит от знака косинуса угла между силой и возможным перемещением.
Положительное значение:
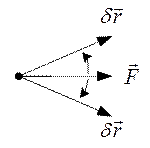

Рис.46
Отрицательное значение:
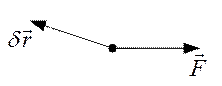

Рис.47
Работа равна нулю, если между направлением силы и возможным перемещение угол прямой.
Виртуальная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижного центра в плоскости, равна произведению момента силы относительно оси вращения на виртуальный угол поворота тела.
7.6 Принцип Лагранжа (Принцип возможных перемещений)
Принцип Лагранжа имеет несколько формулировок и относится к механическим системам, находящимся в равновесии.
Из статики известно, что для равновесия механической системы необходимо и достаточно, чтобы система сил, действующих на каждую точку механической системы, была уравновешена и, чтобы в начальный момент времени механическая система находилась в покое, т.е. чтобы начальные скорости всех точек были нулевыми.
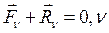 =1,2,…,n. (204)
=1,2,…,n. (204)
Будем предполагать, что последнее условие выполнено.
Формулировка ПВП: для равновесия механической системы, на которую наложены стационарные, голономные, идеальные связи необходимо и достаточно, чтобы алгебраическая сумма виртуальных работ всех активных сил и моментов активных сил на любом возможном перемещении была равна нулю.
SdAакт. = S 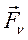 акт.
акт. 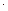 d
d 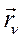 = 0 (205)
= 0 (205)
 2015-05-06
2015-05-06 1166
1166








