Методические рекомендации к решению задач по теме «Теорема об изменении количества движения »

1) выявить совокупность тел, входящих в систему;

2) выбрать систему координат;

3) определить координаты центров масс системы;

4) определить проекции на координатные оси и, если требуется по условиям задачи, модуль скорости центра масс;

5) вычислить проекции на координатные оси, а также модуль и направляющие косинусы вектора количества движения системы;

Примеры решения задач по теме:

Задача № 1

Брус весом Р ₁ перекатывается без скольжения на двух катках весом Р ₂ каждый. Определить количество движения системы, если брус движется со скоростью V₁(рис. 3).

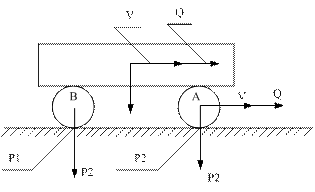
Рис.3

Решение:

Для определения количества движения воспользуемся формулой:

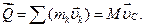(1)

В нашем примере:

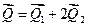(2)

где:

количество движения бруса:

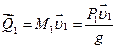(3)

количество движения катка:

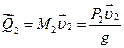(4)

Так как векторы V₁и V₂параллельны, то и векторы Q ₁и Q ₂тоже будут параллельны.

Поэтому модуль количества движения:

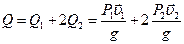(5)

Определим V₂. Так как брус катиться без скольжения то скорости в точках А и В катков будут равны скорости бруса, то есть:

V_A= V_B= V₁.

Так как, катки совершают плоскопараллельное движение, то скорости точек колеса пропорциональны расстояниям до мгновенного центра скоростей, то есть:

.

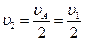Тогда

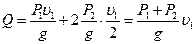. (6)

Задача 2

Человек массой m₁ начинает двигаться по платформе вагонетки с постоянной относительной скоростью 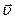. В начальный момент вагонетка массой m₂, находится в покое. Найти скорость движения вагонетки, если её движение происходит в горизонтальной плоскости. Трением скольжения между рельсами и колесами пренебречь (рис.4).

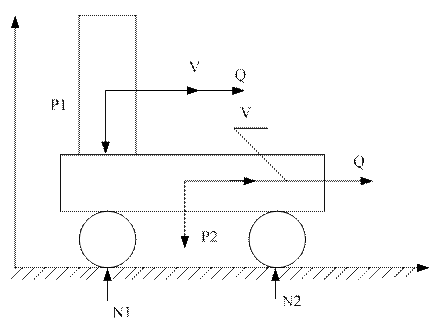
Рис.4

Решение:

Запишем условия в краткой математической форме:

Дано: m₁,m₂,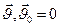

Определить: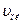

Рассмотрим движение системы, состоящей из человека и платформы (см.рис.4).

Внешние силы: вес платформы 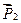, вес человека 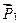, вертикальные реакции .

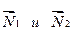Проведем оси координат, направив ось х в сторону движения человека.

Так как 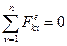(все внешние силы перпендикулярны оси х), то 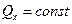, то есть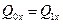

Так как в начальный момент система находилась в покое, то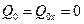

Таким образом,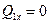

Количество движения системы: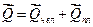

где 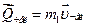- количество движения человека,

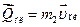- количество движения платформы.

Абсолютная скорость человека (см.рис.4) определяется сложением скорости человека 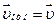и переносной скорости человека, равной скорости платформы,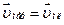

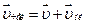, или 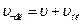, так как векторы скоростей параллельны.

Q_x = Q_{чел x} + Q_{пл x}; (1)

Q_{чел x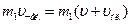} = (2)

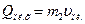(3)

Проекция количества движения на ось х:

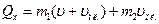(4)

Так как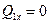

получаем:

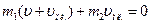(5)

Откуда находим скорость платформы:

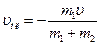(6)

Знак «минус» показывает, что платформа будет двигаться влево.