2015-05-06
2165
• Силы, действующие по прямой, соединяющей частицы, и зависящие только от расстояния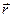 
между ними, называются центральными. Общим для всех центральных сил является следующий закон:
.
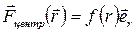При смещении одной из частиц на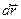 
: 
,
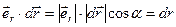т.е. изменение расстояния между частицами.
Отсюда следует, что работа центральной силы:
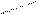2 rdr 
.
er r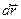
Для любой функции f® результат интегрирования
1 определяется лишь начальным r1 и конечным r2
положениями траектории, и может быть записан так:
.
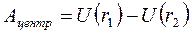• Любая центральная сила является консервативной и частица в поле центральных сил обладает потенциальной энергией.
Примеры центральных сил: гравитационная, кулоновская, упругая силы.
1) Сила гравитационного притяжения.
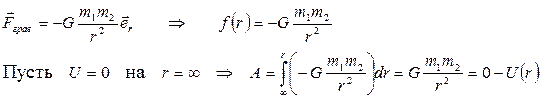
Тогда потенциальная энергия притяжения двух точечных масс имеет вид:
.
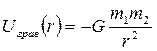2) Кулоновская сила.
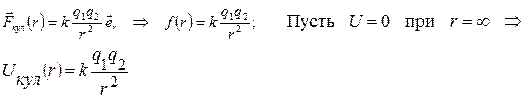
3) Сила упругости.
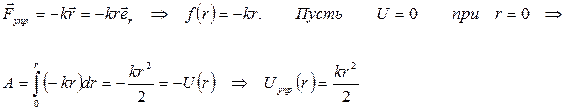
Из определения потенциальной энергии следует:
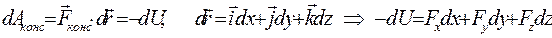
При перемещении вдоль оси Х (когда dy = dz = 0), имеем:
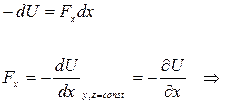
• Проекция консервативной силы на ось ОХ равна частной производной от потенциальной энергии по Х-координате. Аналогично
|
|
|
.
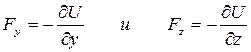Выражение консервативной силы через потенциальную энергию:
.
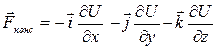Введем оператор «набла»: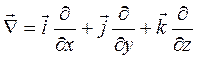 
Þ
.
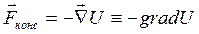Геометрическое место точек, в которых потенциальная энергия частицы (или потенциал) одинакова, называется эквипотенциальной поверхностью.
Уравнение такой поверхности: U | s = const.
При перемещении по этой поверхности dU = 0, и из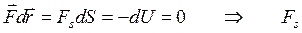 
= 0
То есть, проекция силы на эквипотенциаль всегда равна нулю.
Поэтому
• вектор консервативной силы всегда перпендикулярен эквипотенциальной поверхности.
Если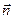 
– единичный вектор нормали к эквипотенциальной поверхности, то Fn = - ¶U/¶n ¶U/¶n > 0, Fn < 0 Þ
• вектор консервативной силы всегда направлен в сторону убывания (уменьшения) потенциальной энергии, и в том же направлении под действием силы будут ускоряться все тела. Вектор grad U направлен по нормали к эквипотенциальной поверхности, но противоположно силе.
3.5. Механическая энергия частицы и закон ее сохранения.
Неконсервативные силы
Полная механическая энергия частицы: E = K + U.
Если на частицу действуют только консервативные силы, то с одной стороны dA = – dU, с другой (из второго закона Ньютона): dA = dK Þ – dU = dK d(K + U) = dE = 0 Þ
• механическая энергия частицы, подверженной действию только консервативных сил, сохраняется.
Неконсервативные силы – силы, работа которых зависит от длины и формы пути. То есть, работа неконсервативных сил на замкнутом пути не равна нулю, с ними не связана потенциальная энергия.
Примеры: сила трения скольжения, сила вязкого трения.
Работа силы трения скольжения зависит не от перемещения тела, а от длины пути: Aтр = - mNl и не равна нулю при возвращении тела в исходную точку.
|
|
|
Пусть на частицу действуют как консервативные, так и неконсервативные силы. Уравнение движения этой частицы будет иметь вид:
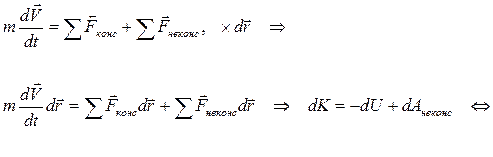
dE = d(K + U) = dAнеконс.
• Изменение полной механической энергии частицы равно работе всех действующих на нее неконсервативных сил:
.
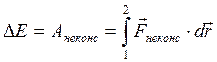При этом изменение механической энергии в замкнутой системе компенсируется изменением тепловой, химической и других видов энергии.
Разделим почленно закон изменения энергии на dt
.
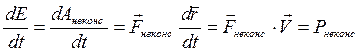• скорость изменения полной механической энергии равна мощности неконсервативных сил.
Важный случай неконсервативных сил – диссипативные силы – силы, зависящие от скорости частицы и направленные против скорости:
.
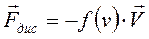Пример – сила вязкого трения.
4. МОМЕНТ ИМПУЛЬСА. ДИНАМИКА СИСТЕМЫ ЧАСТИЦ.
ЗАКОНЫ СОХРАНЕНИЯ
