На конечном перемещении. Мощность

Работа постоянной силы на прямолинейном перемещении (рис. 14) равна скалярному произведению вектора силы на вектор перемещения:

A = F∙s∙cosα.

Если сила, действующая на точку, является переменной или её перемещение является криволинейным (рис. 15), то в этом случае вводится понятие элементарной работы силы dA, которой называется работа силы на бесконечно малом перемещении. Поскольку бесконечно малое перемещение можно считать прямолинейным, а силу на этом перемещении постоянной, то

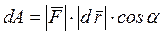. Соответственно элементарная работа силы равна скалярному произведению вектора силы на вектор элементарного перемещения: 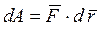. Если раскрыть скалярное произведение, то получим

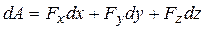. (28)

Учитывая, что направление вектора 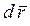в пределе совпадает с направлением вектор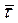а , а 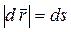, получим еще одну формулу: .

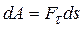Работа силы на конечном перемещении М₀М₁ равна взятому вдоль этого перемещения интегралу от элементарной работы:

.

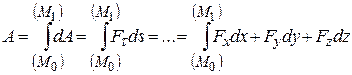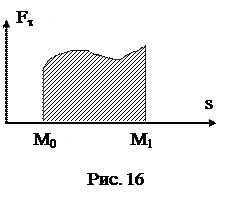
Геометрически работа силы равна площади криволинейной трапеции (рис. 16).

Средней мощностью силы называется отношение работы силы к промежутку времени, за который она совершена: 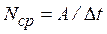. Мощностью силы в данный момент называется отношение элементарной работы к бесконечно малому промежутку времени: 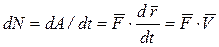, т.е. мощность силы равна скалярному произведению вектора силы на скорость. Работа измеряется в джоулях, а мощность в ваттах. 1 Дж = 1 Н∙м. 1Вт = 1 Дж/с.