Уравнения Колмогорова

Случайный процесс называется Марковским (или процессом без последействия), если для каждого момента времени t₀ вероятность любого состояния системы в будущем (при t>t₀) зависит только от ее состояния в настоящем (при t=t₀) и не зависит от того, когда и каким образом система пришла в это состояние

Поскольку множество возможных состояний систем массового обслуживания дискретно (S₁, S₂,...,S_n), процесс, протекающий в них, является процессом с дискретными состояниями. В некоторые моменты времени система скачком переходит из одного состояния в другое. Изменение состояний происходит мгновенно, в случайные моменты времени, а число возможных состояний конечно. Протекание процесса определяется вероятностями перехода из некоторого состояния i в состояние j (при конечном числе состояний i=0..n, j=0..n).

Рассмотрим процесс, протекающий в двухканальной системе массового обслуживания. Определим множества состояний, в которых может оказаться система. В данном случае каждый из каналов может находиться в двух состояниях: занятом или свободном. Следовательно, система имеет три возможных состояния: S₀ - оба канала свободны, S₁ - один канал (безразлично, какой именно) занят, S₂ - оба канала заняты.

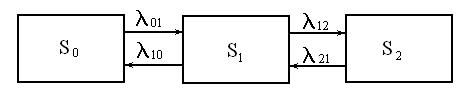
Случайный процесс, протекающий в системе, можно представить в виде графа состояний. Направления переходов обозначаются стрелками. Изменения состояний слева направо происходит под действием входящего потока, а справа налево – вследствие освобождения каналов обслуживания. Полагаем, что потоки событий простейшие, поэтому одновременный приход двух вызовов или одновременное освобождение двух каналов невозможен (переходы из состояния S₀ в состояние S₂ и обратно запрещены, т.е. l₀₂=l₂₀=0). Граф состояний системы с указанными интенсивностями переходов называют размеченным графом состояний.

Вероятности нахождения системы в различных состояниях являются исходной информацией для определения показателей эффективности системы массового обслуживания. Эти вероятности можно найти из так называемых уравнений Колмогорова. Их легко составить по известному размеченному графу состояний. Покажем это на примере графа.

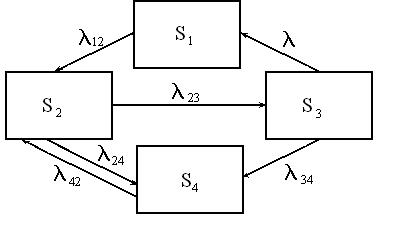
Как было показано, для малых интервалов времени (Dt<<max [1/l _ij ]) вероятность перехода из состояния i в состояние j p _ij (Dt)»l _ij ×Dt (i¹j). Поставим задачу найти вероятность p₁(t), то есть вероятность нахождения системы в состоянии S₁ в момент t. Дадим малое приращение Dt и найдем вероятность того, что система окажется в состоянии S₁ в момент t+Dt.

Имеются два варианта реализации этого события:

- в момент t система уже была в состоянии S₁, за время Dt состояние системы не изменилось;

- в момент t система находилась в состоянии S₃ и в течение Dt перешла из состояния S₃ в состояние S₁.

Других вариантов нет, поскольку:

- с этим состоянием связаны только две стрелки переходов, остальные переходы запрещены (их интенсивность равна нулю);

- два и более переходов за малый интервал времени Δt произойти не могут т.к. потоки событий полагаются простейшими.

Вероятность первого варианта равна p₁(t)×(1-l₁₂Dt), вероятность второго - p₃(t)× l₃₁Dt. Применяя правило сложения вероятностей, получим

p₁(t+Dt)= p₁(t)×(1-l₁₂Dt)+ p₃(t)× l₃₁Dt.

Откуда

.

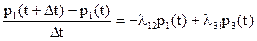Переходя к пределу при Dt®0, получим дифференциальное уравнение, которому должна удовлетворять вероятность p₁(t):

.

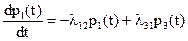Пользуясь этой же методикой, найдем дифференциальное уравнение для вероятности p₂(t). Найдем вероятность p₂(t+Dt), то есть вероятность того, что система окажется в состоянии S₂ в момент t+Dt. Это событие может произойти следующимиспособами:

- В момент t система уже была в состоянии S₂ , за время Dt состояние системы не изменилось. Вероятность этого события равна

p₂(t) ×(1- l₂₃Dt - l₂₄ Dt).

- В момент t система находилась в состоянии S₁ и за время Dt перешла из состояния S₁ в состояние S₂. Вероятность этого события равна p₁ (t)× l₁₂×Dt.

- В момент t система находилась в состоянии S₄ и за время Dt перешла из состояния S₄ в состояние S₂. Вероятность этого события равна p₄ (t)× l₄₂×Dt.

Поскольку за время Dt (Dt<<max[1/l_ij]) вероятность двух и более переходов пренебрежимо мала, искомая вероятность

p₂(t+Dt)= p₂(t) ×(1- l₂₃ Dt- l₂₄ Dt)+p₁(t)× l₁₂Dt+ p₄(t)× l₄₂Dt.

Проделав преобразования и перейдя к пределу при Dt®0, получим дифференциальное уравнение, которому должна удовлетворять вероятность p₂(t):

.

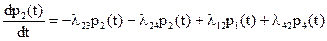Рассуждая аналогично, получим систему дифференциальных уравнений (уравнения Колмогорова):

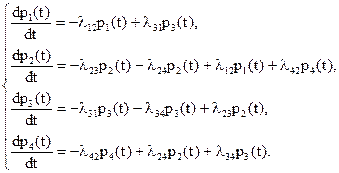
Число уравнений равно числу возможных состояний. Интегрирование системы дает искомые вероятности. Начальные условия определяются постановкой задачи. Например, если известно, что при t=0 система находилась в состоянии S₁, то начальные условия определяются как p₁(0)=1, p_i(0)=0, i= 2, 3, 4.

Матрица интенсивностей переходов, соответствующая размеченному графу состояний, имеет вид:

.

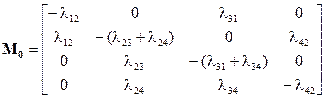Уравнения Колмогорова отражают, в частности, тот факт, что в стационарном режиме (все вероятности p_k(t)=p_k - постоянны) интенсивность перехода системы из некоторого состояния k в любое другое равна суммарной интенсивности перехода в состояние k из всех других состояний. Это значит, что сума элементов любого столбца матрицы M₀ равна нулю.

Полагается, что переход из оного состояния в другое происходит мгновенно. Поэтому вероятности состояний образуют полную группу несовместимых событий, и, следовательно, помимо уравнений Колмогорова для любого момента времени справедливо т.н. уравнение нормировки

p₁(t)+ p₂(t)+ p₃(t)+ p₄(t) =1.

Отсюда следует, что, по известному размеченному графу состояний системы можно записать систему уравнений Колмогорова, пользуясь простыми правилами [4]:

1) Число уравнений равно числу возможных состояний системы.

2) В левой части каждого уравнения стоит производная по времени вероятности состояния, а правая часть содержит столько слагаемых, сколько стрелок связано с данным состоянием.

3) Если стрелка направлена из состояния, соответствующий член имеет знак «минус», если в состояние - знак «плюс».

4) Каждое слагаемое равно произведению интенсивности перехода, соответствующего данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.

Отметим, что задача составления размеченного графа состояний может оказаться достаточно сложной.