Ортогональная аппроксимация

В этом случае, как правило, выбирается критерий среднеквадратичного приближения и некоторая система ортогональных базисных функций .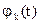

Координатами функции 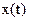являются коэффициенты ее разложения в ряд по системе базисных функций 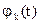. Возможен также выбор в качестве координат мгновенных значений (отсчетов) функции , k=0, 1 и т.д.

Условие ортогональности функций имеет вид

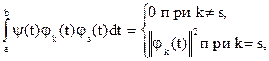
где 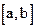– интервал ортогональности; 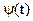– некоторая весовая функция; 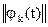– норма k-й базисной функции.

При 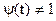имеем ортогональность функций с весом. Для некоторых систем вес 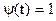. Если норма 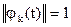, то базис кроме ортогональности является еще и нормированным. А в целом –это ортонормированный базис.

Известно много систем ортогональных функций. Например, полиномы Чебышева, Лежандра, Котельникова, Лагера, Эрмита, Якоби, Уолша, Хаара и др. Примером ортонормированных функций с весом 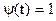может служить базис тригонометрического ряда Фурье:

.

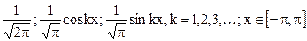Ортогональное разложение дает наименьшую среднеквадратичную погрешность, когда коэффициенты разложения вычисляются как обобщенные коэффициенты Фурье функции 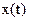, т.е.

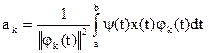. (2.10.2)

Представление сигнала 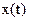рядом (2.10.1) с коэффициентами (2.10.2) является оптимальным, так как минимизирует число координат и погрешность .

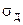Рассмотрим выбор ортогональных функций. Следует выбирать систему функций, которая обеспечивает быструю сходимость ряда (2.10.1). В результате при заданной погрешности аппроксимации будет наименьшее число членов ряда (степень n). Однако в технике решающим фактором является простота генератора базисных функций ГБФ. Этому условию удовлетворяют тригонометрические функции, функции Уолша и Хаара. Этим объясняется их широкое применение.