Функции Уолша 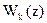 ортогональны на отрезке
ортогональны на отрезке 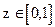 с весом
с весом 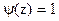 . Известны четыре формы их записи и построения. Мы рассмотрим две.
. Известны четыре формы их записи и построения. Мы рассмотрим две.
1. Систему Уолша можно построить на базе системы функций Радемахера

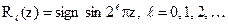 ,
,
где 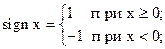
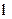 – порядок функции Радемахера.
– порядок функции Радемахера.
Функции Радемахера ортонормированы:
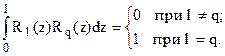
Вид четырех функций Радемахера показан на рис.2.70. Генерируются они технически просто – обычным двоичным счетчиком.
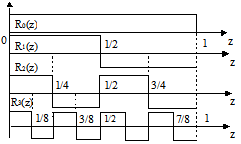
Рис.2.70
Однако система Радемахера неполная. По ней можно разложить не любой сигнал, а только нечетный, так как функции Радемахера – нечетные.
Дополнение системы Радемахера приводит к системе Уолша. Эта система строится следующим образом. Для получения k-й функции Уолша 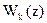 число k представляется в двоичной системе счисления, т. е.
число k представляется в двоичной системе счисления, т. е.
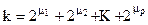 ,
,
где 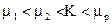 – целые числа.
– целые числа.
Функция Уолша определяется формулой
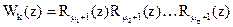 .
.
Для функции нулевого порядка принимается 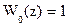 .
.
Например, 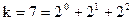 . Отсюда следует
. Отсюда следует 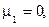
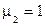 и
и 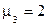 . Тогда функция Уолша 7-го порядка будет (рис.2.71)
. Тогда функция Уолша 7-го порядка будет (рис.2.71)
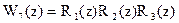 .
.
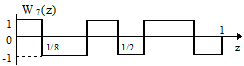
Рис.2.71
График четырех функций Уолша приведен на рис.2.72.
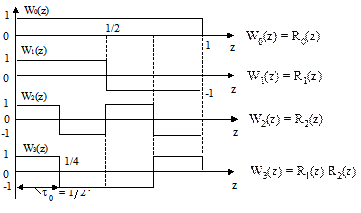
Рис.2.72
Из функций Радемахера порядка 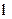 можно построить
можно построить  функций Уолша.
функций Уолша.
2. Второй способ построения систем функций Уолша. В основе этого способа лежат свойства матриц Адамара. Полученная система называется системой Уолша - Адамара.
Элементарная матрица Адамара состоит из одного элемента 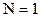 и имеет вид
и имеет вид 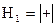 . Для
. Для 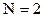 имеем базисную матрицу Адамара
имеем базисную матрицу Адамара
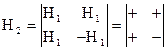 , где
, где 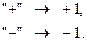
Для 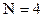 матрица имеет ту же структуру, но с элементами
матрица имеет ту же структуру, но с элементами 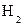 :
:
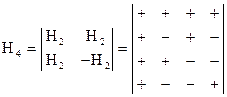 .
.
Для 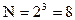 имеем матрицу Адамара с элементами
имеем матрицу Адамара с элементами 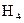 :
:
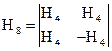 и т. д.
и т. д.
Процесс наращивания матрицы продолжают до получения матрицы с нужным числом базисных функций.
Функции Уолша хороши тем, что они достаточно просто реализуются аппаратурно. В качестве примера рассмотрим структуру генератора 8-ми функций Уолша. Составим систему функций Уолша на базе системы функций Радемахера:
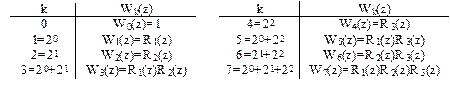
Таким образом, для формирования функций Уолша требуется генератор трех функций Радемахера, включающий задающий генератор G, два счетных триггера T1 и T2, а также устройства умножения соответствующих функций Радемахера (рис.2.73). Функция Уолша нулевого порядка W0(z)=R0(z) формируется источником постоянного напряжения с единичным уровнем.
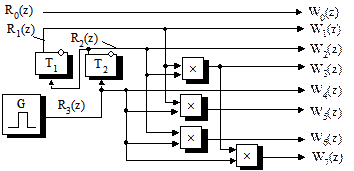
Рис.2.73
Техническая реализация умножения функций Радемахера может быть заменена логическими операциями.
а) Обозначим: уровень 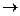 символ
символ
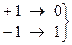 отрицательная логика.
отрицательная логика.
Тогда умножению соответствует логическая операция сложение по mod2:
| умножение | сложение по mod2 |
| (1)´(1)= 1 | 0 Å 0= 0 |
| (1)´(-1)= -1 | 0 Å 1= 1 |
| (-1)´(1)= -1 | 1 Å 0= 1 |
| (-1)´(-1)= 1 | 1 Å 1= 0 |
б) Обозначим: уровень 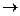 символ
символ
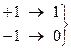 положительная логика.
положительная логика.
Здесь умножению будет соответствовать функция алгебры логики (ФАЛ) “равнозначность”.
Таким образом, в зависимости от типа выбранной логики устройства умножения будут представлять собой или устройства сложения по mod2 или устройства, реализующие ФАЛ “равнозначность”.
Произвольный интервал 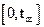 задания функции
задания функции 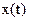 всегда можно привести к интервалу ортогональности
всегда можно привести к интервалу ортогональности 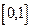 . Для этого нужно сделать замену переменной
. Для этого нужно сделать замену переменной 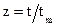 , где
, где 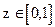 .
.
 2015-05-06
2015-05-06 3883
3883








