Пусть на точку М,кроме восстанавливающей силы 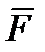 , направленной к центру О,действует еще и постоянная по модулю и направлению сила
, направленной к центру О,действует еще и постоянная по модулю и направлению сила 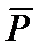 (рис. 9.2). В этом случае положением равновесия точки М будет центр О1, отстоящий от О на расстоянии ОО1 = dст, которое определяется равенством
(рис. 9.2). В этом случае положением равновесия точки М будет центр О1, отстоящий от О на расстоянии ОО1 = dст, которое определяется равенством 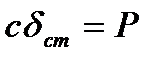 или
или
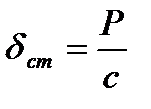 . (9.10)
. (9.10)
Величина dст называется статическим отклонением точки.
Примем центр О1 за начало отсчета, координатную ось О1 x направим в сторону действия силы 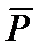 , тогда получим
, тогда получим 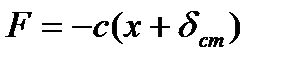 . Учитывая, что
. Учитывая, что 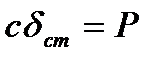 , получим дифференциальное уравнение движения в виде
, получим дифференциальное уравнение движения в виде
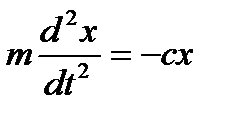 или
или 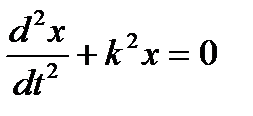 .
.
То есть постоянная сила 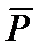 не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы
не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы 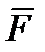 , а только смещает центр этих колебаний в сторону действия силы
, а только смещает центр этих колебаний в сторону действия силы 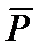 на величину статического отклонения dст.
на величину статического отклонения dст.
С учетом того, что 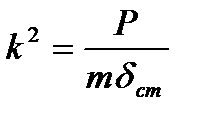 , выражение (9.7) примет вид
, выражение (9.7) примет вид
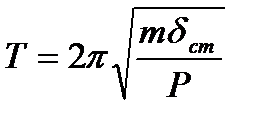 . (9.11)
. (9.11)
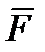 , направленной к центру О,действует еще и постоянная по модулю и направлению сила
, направленной к центру О,действует еще и постоянная по модулю и направлению сила 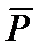 (рис. 9.2). В этом случае положением равновесия точки М будет центр О1, отстоящий от О на расстоянии ОО1 = dст, которое определяется равенством
(рис. 9.2). В этом случае положением равновесия точки М будет центр О1, отстоящий от О на расстоянии ОО1 = dст, которое определяется равенством 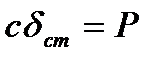 или
или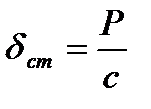 . (9.10)
. (9.10)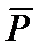 , тогда получим
, тогда получим 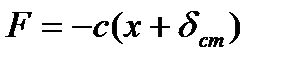 . Учитывая, что
. Учитывая, что 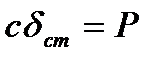 , получим дифференциальное уравнение движения в виде
, получим дифференциальное уравнение движения в виде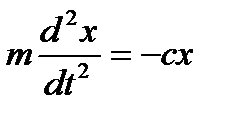 или
или 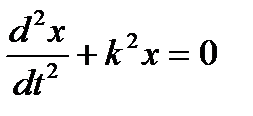 .
.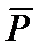 не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы
не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы 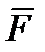 , а только смещает центр этих колебаний в сторону действия силы
, а только смещает центр этих колебаний в сторону действия силы 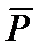 на величину статического отклонения dст.
на величину статического отклонения dст.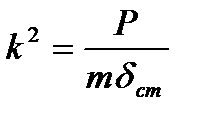 , выражение (9.7) примет вид
, выражение (9.7) примет вид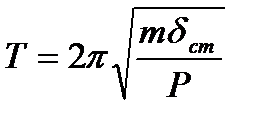 . (9.11)
. (9.11) 2015-04-20
2015-04-20 1454
1454








