Затухающие колебания. Пусть материальная точка Мдвижется прямолинейно по оси x

Пусть материальная точка М движется прямолинейно по оси x. На точку при ее движении действуют восстанавливающая сила 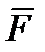и сила сопротивления 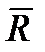(рис. 9.3). Считая, что сила сопротивления пропорциональна первой степени скорости: 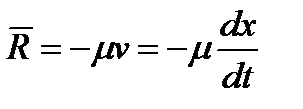, , 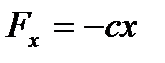получим дифференциальное уравнение движения в виде

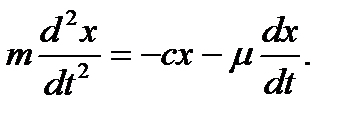(9.12)

Разделив обе части уравнения на m и вводя обозначения 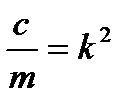и 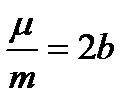, приведем уравнение к виду

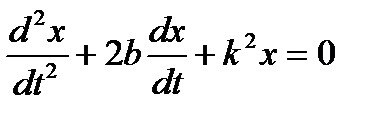. (9.13)

О

М

x

F

R

v

Рис. 9.3

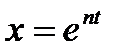Уравнение (9.13) представляет собой дифференциальное уравнение свобод­ных колебаний при сопротивлении про­порциональном скорости. Его решение, как и решение уравнения (9.3), ищут в виде . Подставляя это значение x в уравнение (9.13), получим характери­стическое уравнение 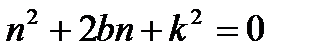, корни которого будут

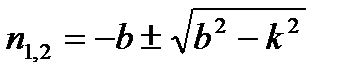. (9.14)

Рассмотрим случай, когда k > b, то есть когда сопротивление мало по сравнению с восстанавливающей силой. Введем обозначение

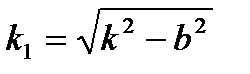, (9.15)

получим из (9.14), что 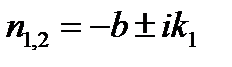, то есть корни характеристического уравнения являются комплексными. Тогда решение уравнения (9.13) будет иметь вид

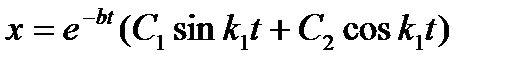(9.16)

или, по аналогии с равенством (9.5),

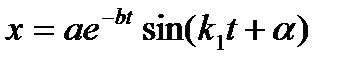. (9.17)

Величины а и a являются постоянными интегрирования и определяются по начальным условиям.

0

t

x

x1

x2

T1

Рис. 9.4

Колебания, происходящие по закону (9.17), называют затухающими, так как благодаря наличию множителя е^-bt величина x = ОМ с течением времени убывает стремясь к нулю. График этих колебаний показан на рис. 9.4.

Промежуток времени Т₁, рав­ный периоду 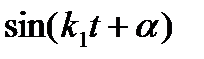называют периодом затухающих колебаний.

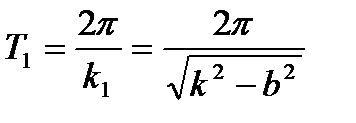, (9.18)

Если учесть равенство (9.7), формулу (9.18) можно представить в виде

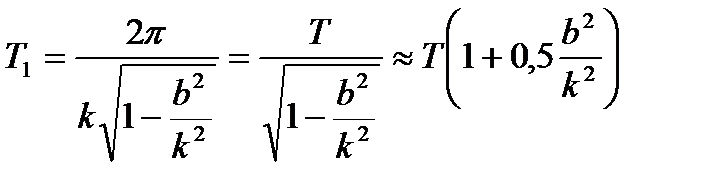. (9.19)

Из полученных зависимостей видно, что Т₁> Т, то есть при наличии сопротивления период колебаний несколько увеличивается. Но если сопротивление мало (b<< k), то величиной 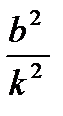по сравнению с единицей можно пренебречь и считать Т₁» Т.

Промежуток времени между двумя последовательными отклонениями колеблющейся точки также равен Т₁. Следовательно, если первое максимальное отклонение x₁ происходит в момент времени t₁, то второе отклонение x₂ наступит в момент t₂ = t₁+ Т₁ и т. д. Тогда, учитывая, что 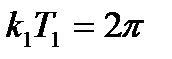, из формулы (9.17) получим:

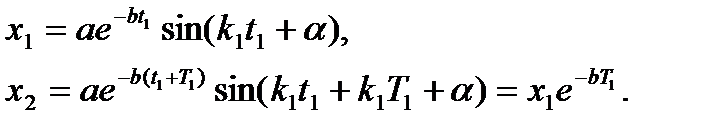
Аналогично для любого отклонения x_n+1 будет 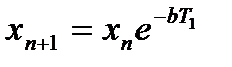. Таким образом, абсолютные значения отклонений колеблющейся точки М от центра О убывают по закону геометрической прогрессии. Знаменатель этой прогрессии 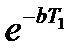называется декрементом затухающих колебаний, а натуральный логарифм декремента – величина bT₁, называется логарифмическим декрементом.

Из полученных результатов следует, что малое сопротивление почти не влияет на период колебаний, но вызывает их постепенное затухание.

В случаях, когда b> k или b= k движение точки является апериодическим, то есть оно уже не имеет характера колебательного движения.