2015-04-20
500
Для того щоб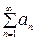 
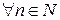зб. Необхідно і достатньо 
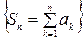- обмежена
Признаки сходимости:
1. Признак сравнения. Если два ряда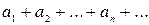 
и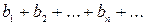 
имеют положительные члены и, начиная с некоторого n, 
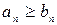, то из сходимости первого ряда следует сходимость второго, а из расходимости второго ряда следует расходтмость первого.
2. Признак сравнения в предельной форме. Если существует придел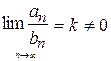 
. Тогда первый ряд эквивалентен второму (т.е. ведут себя одинаково).
Интегральный признак Коши-Маклорена. Пусть ф-я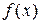 
неотрицательна и невозрастает на [1,+ 
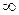), тогда ряд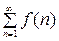 
3. и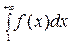 
ведут себя одинаково. (ф-я невозрастает на (а,b), если для любых 
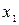и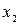 
: 
: 
).
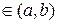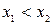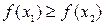4. Признак Даламбера. 1) Если начиная с некоторого номера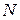 
для любого 
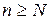вып-ся 
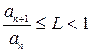,то ряд – сх-ся, если это отношение 
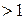, то ряд – расх-ся. 2) Если 
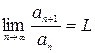, то при 
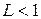- ряд сходится, при 
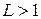- ряд расх-ся, 
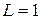- нельзя сказать.
5. Признак Коши. 1) Если начиная с некоторого номера 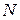для любого 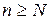вып-ся 
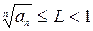,то ряд – сх-ся, если это отношение 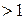, то ряд – расх-ся. 2) Если 
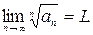, то при 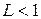- ряд сх-ся, при 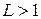- ряд расх-ся, 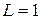- нельзя сказать.
Абсолютная и условная сходимость.
