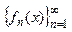 - функц-я последовательность (ФП),
- функц-я последовательность (ФП), 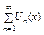 - функц-й ряд (ФР).
- функц-й ряд (ФР).
Опр. 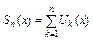 .
. 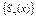 - ФП.
- ФП.
1.Область опр-я ФП – мн-во Х, при котором Для любого 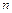 :
: 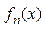 имеет смысл.
имеет смысл.
2.Область сх-ти ФП – мн-во тех Х, при кот. числовая посл-ть 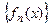 - сх-ся.
- сх-ся.
3. 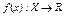 наз. предельной функцией, если для любого
наз. предельной функцией, если для любого 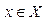
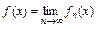 , т.е.
, т.е. 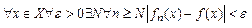 .
.
4. 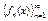 наз. равномерносх-ся к
наз. равномерносх-ся к 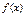 на мн-ве Х,
на мн-ве Х, 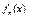 равном-но сх-ся а
равном-но сх-ся а 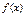 , если
, если 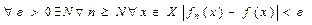 .
.
5.Критерий равномерной сх-ти. 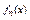 равном-но сх-ся а
равном-но сх-ся а 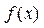
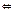
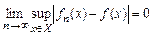 .
.
6.Криткрий Коши (равномерной сх-ти). ФП 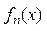 равномерно на мн-ве Х стремится к нек. предельной ф-и
равномерно на мн-ве Х стремится к нек. предельной ф-и 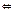
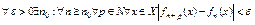 .
.
Опр. Ряд составленный из функций одной и той же переменной 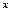 :
: 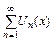 , наз. функциональным.
, наз. функциональным.
Опр. ФР наз. равномерносходящимся на Х, если на этом мн-ве равномерно сх-ся посл-ть его частичных сумм.
Критерий Коши равн-ой сх-ти ФР: 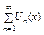 - равн-но сх-ся
- равн-но сх-ся 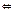
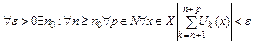 .
.
Признаки равномерной сх-ти ФР:
1.Признак Веерштраса. ФР равномерно сх-ся в области Х, если сущ. такой сх-ся числовой ряд 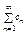 , что для всех значений
, что для всех значений 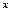 , лежащих в этой области, имеет место неравенство
, лежащих в этой области, имеет место неравенство 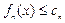 .
.
2.Признак Дирихле. Пусть на Х частичный 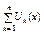 равномерно ограничен, а последовательность
равномерно ограничен, а последовательность 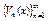 монотонна (т.е.
монотонна (т.е. 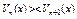 ) при каждом
) при каждом 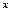 и равномерно сх-ся к 0 на Х, тогда
и равномерно сх-ся к 0 на Х, тогда 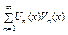 -равномерно сх-ся на Х.
-равномерно сх-ся на Х.
3.Признак Абеля. Пусть 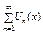 -равномерно сх-ся, а
-равномерно сх-ся, а 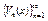 монотонна при каждом
монотонна при каждом 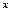 и равномерно ограничена, тогда
и равномерно ограничена, тогда 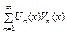 -равномерно сх-ся на Х.
-равномерно сх-ся на Х.
Свойства функциональных рядов.
1.Почленное интегрирование
Теорема (для рядов): Пусть для любого 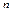
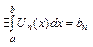 , и пусть
, и пусть 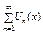 -равномерно сх-ся на
-равномерно сх-ся на 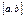 к
к 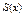 , тогда
, тогда 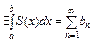
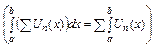 .
.
Теорема (для последовательности): Пусть для любого 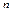
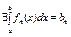 , и пусть
, и пусть 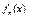 -равномерно сх-ся на
-равномерно сх-ся на 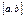 к
к 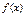 , тогда
, тогда 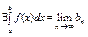
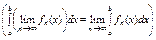 .
.
 2015-04-20
2015-04-20 746
746








