Среди мн-нов от нескольких переменных выделяются те, которые не меняются ни при какой перестановке неизвестных. В такие мн-ны все неизв. входят симметричным образом и поэтому эти мн-ны назыв. симметрическими мн-нами (или симметрическими функциями).
Простыми примерами будут: сумма всех неизв. 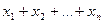 сумма квадратов неизв.
сумма квадратов неизв. 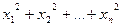 , произведение неизвестных
, произведение неизвестных 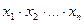 и т. д.
и т. д.
Будем рассматривать сим. мн-ны от 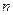 неизвестных с коэф.-тами из некоторого поля
неизвестных с коэф.-тами из некоторого поля 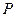 сумма разность, произведение сим. мн-нов сами будут сим. мн-нами, т. е. сим. мн-ны составляют подкольцо в кольце
сумма разность, произведение сим. мн-нов сами будут сим. мн-нами, т. е. сим. мн-ны составляют подкольцо в кольце  всех мн-нов от
всех мн-нов от 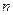 неизв. над полем
неизв. над полем 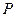 называется кольцом симметр-ких мн-нов от
называется кольцом симметр-ких мн-нов от 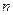 неизв. над полем
неизв. над полем 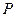 .
.
К этому кольцу принадлежат все эл-ты из 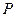 (мн-ны нулевой степени). Всякий другой сим. мн-н непримерно содержит вес
(мн-ны нулевой степени). Всякий другой сим. мн-н непримерно содержит вес 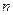 неизв. и даже имеет по ним одну и ту же степень: если сим. мн-н
неизв. и даже имеет по ним одну и ту же степень: если сим. мн-н 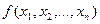 обладает членом в который неизв.
обладает членом в который неизв. 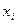 входит с показателем
входит с показателем 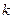 , то он обладает и членом, получ. из неготранспозицией неизвестных,
, то он обладает и членом, получ. из неготранспозицией неизвестных, 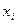 и
и 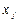 т. е. содержащие неизв.
т. е. содержащие неизв. 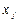 в той же степени
в той же степени 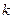 .
.
Следующие 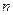 сим. мн-нов от
сим. мн-нов от 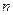 неизвестных назыв. элементарными сим. мн-нами
неизвестных назыв. элементарными сим. мн-нами 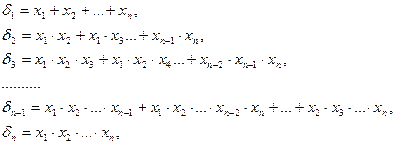
Т. к. сим. мн-ны от 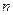 неизвестных
неизвестных 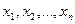 над полем
над полем 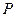 составляют кольцо, то очевидно след. утв. сим-ким мно-ном будет всякая целая положит. степень любого из элементов сим. мн-нов, а также произведение таких степеней, притом взятое с любым коэф-том из
составляют кольцо, то очевидно след. утв. сим-ким мно-ном будет всякая целая положит. степень любого из элементов сим. мн-нов, а также произведение таких степеней, притом взятое с любым коэф-том из 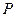 ,
, 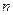 , наконец, всякая сумма указанных произведений. Иными словами всякий мн-н от элементарных сим. мн-нов
, наконец, всякая сумма указанных произведений. Иными словами всякий мн-н от элементарных сим. мн-нов 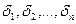 с коэф-тами из
с коэф-тами из 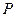 , рассматиривается как мн-н от неизвестных
, рассматиривается как мн-н от неизвестных 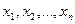 будет сим-ким.
будет сим-ким.
Пусть 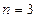 и возьмем мн-член
и возьмем мн-член 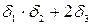 заменяя
заменяя 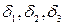 их выражения, получим:
их выражения, получим: 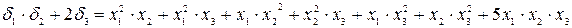 справа стоит очевидно сим-кий мн-н от
справа стоит очевидно сим-кий мн-н от 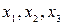 .
.
Обращением этого результата явл, основная теорема о сим-ких мн-нах: «любой сим-кий мн-н от n-переменных может быть выражен через основные сим. мн-ны от n-переменных».
65. Не приводимые многочлены над Q, R, С
Мн-н называется не приводимым над полем Р, если не может быть представлен в виде произведения двух других мн-нов с коэф-ми из поля Р, степени которых меньше степени данного мн-на.
Мн-н нулевой степени (const) не причисляется ни к приводимым, ни к не приводимым.
Над полем С не приводимы только мн-ны первой степени. Всякий мн-н может быть разложен на лин-ые множители, т.е. всякий мн-н в виде: a0xn+ a1xn-1+…
Над полем R не приводимы только мн-ны 1-ой степени и мн-ны 2-ой степени, не имеющие действит.корней.
Над полем Q существуют не приводимые мн-ны различных степеней.
Пример: xn+2, nєN.
Непроводимость мн-на над Q определяется по критерию Эйзенштейна: Если для мн-на n>0 с целыми коэф-ми существует простое число p: старший коэф-т 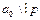 , все остальные коэф-ты
, все остальные коэф-ты 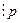 , а свободный член
, а свободный член 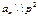 ,
, 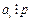 i=1,n. То этот мн-н – не приводим над полем Q.
i=1,n. То этот мн-н – не приводим над полем Q.
Пример: 1) x4+1 – над Q. 2) x4+1= 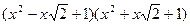 - над R. 3)
- над R. 3) 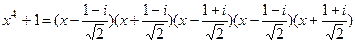 - над С.
- над С.
Если степень мн-на > 0 => не разрешимые в радикалах.
 2015-04-20
2015-04-20 651
651








