Теорема о «двух милиционерах»

Теорема о существовании предела функции, которая «зажата» между двумя другими функциями, имеющими одинаковый предел. Формулируется следующим образом:

Если функция 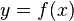такая, что 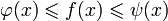для всех 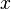в некоторой окрестности точки 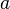, причем функци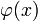и и 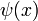имеют одинаковый предел при 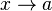, то существует предел функци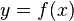и при 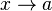, равный этому же значению, то есть

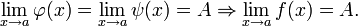
Теорема о пределе монотонной ограниченной последовательности

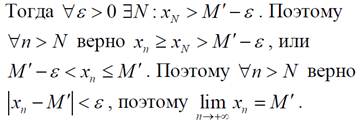
Теорема о вложенных отрезках (о стягивающейся системе сегментов)

Теорема Больцано-Вейерштрасса

Критерий Коши сходимости последовательности

Теоремы с доказательством

Докажите, что сходящаяся последовательность имеет один предел