2018-01-08
2422
Функция 
называется бесконечно малой при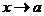 
или при 
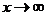, если 
или 
.
Например: функция 
бесконечно малая при 
; функция 
бесконечно малая при .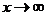
Замечание 1. Никакую функцию без указания направления изменения аргумента бесконечно малой назвать нельзя. Так, функция 
при является бесконечно малой, а при 
она уже не является бесконечно малой (
).
Замечание 2. Из определения предела функции в точке, для бесконечно малых функций выполняется неравенство 
.Этим фактом мы в дальнейшем будем неоднократно пользоваться.
Установим некоторые важные свойства бесконечно малых функций.
Теорема (о связи функции, её предела и бесконечно малой): Если функция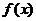 
может быть представлена в виде суммы постоянного числа А и бесконечно малой функции 
при 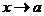, то число 
Доказательство:
Из условия теоремы следует, что функция 
.
Выразим отсюда : 
. Поскольку функция бесконечно малая, для неё справедливо неравенство , тогда для выражения (
) также выполняется неравенство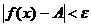 
А это значит, что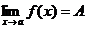 
.
Теорема (обратная): если 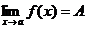, то функция 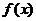может быть представлена в виде суммы числа А и бесконечно малой при 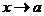функции , т.е. .
Доказательство:
Так как 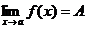, то для 
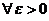выполняется неравенство
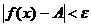(*) Рассмотрим функцию как единую и неравенство (*) перепишем в виде 
Из последнего неравенства следует, что величина () является бесконечно малой при 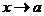. Обозначим её .
Откуда . Теорема доказана.
Теорема 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Доказательство:
Проведём доказательство для двух слагаемых, так как для любого конечного числа слагаемых оно приводится аналогично.
Пусть и 
бесконечно малые при 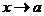функции и 
– сумма этих функций. Докажем, что для 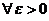, существует такое 
, что для всех х, удовлетворяющих неравенству 
, выполняется неравенство 
.
Так как функция 
бесконечно малая функция, 
, а следовательно существует такое 
, что для всех 
выполняется неравенство 
.
Так как функция 
бесконечно малая функция, 
, а следовательно существует такое 
, что для всех 
выполняется неравенство 
.
Возьмём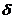 
равным меньшему из чисел и , тогда в 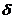–окрестности точки а будут выполняться неравенства , .
Составим модуль функции 
и оценим его значение.
. то есть , тогда функция бесконечно малая, что и требовалось доказать.
Теорема 2. Произведение бесконечно малой функции 
при 
на ограниченную функцию 
есть бесконечно малая функция.
Доказательство:
Так как функция ограниченная, то существует такое положительное число 
, что для всех 
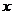выполняется неравенство 
.
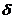Так как функция бесконечно малая при , то существует такая –окрестность точки 
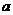, что для всех 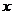их этой окрестности выполняется неравенство 
.
Рассмотрим функцию 
и оценим её модуль
Итак 
, а тогда – бесконечно малая.
Теорема доказана.
Теоремы о пределах.
Теорема 1. Предел алгебраической суммы конечного числа функций равен алгебраической сумме пределов этих функций
.
Доказательство:
Для доказательства достаточно рассмотреть две функции, это не нарушит общности рассуждений.
Пусть 
, 
.
По теореме о связи функции, её предела и бесконечно малой, функции 
и 
можно представить в виде 
где и 
– бесконечно малые при .
Найдём сумму функций и
Величина 
есть постоянная величина, 
– величина бесконечно малая. Таким образом, функция 
представлена в виде суммы постоянной величины и бесконечно малой функции.
Тогда число 
является пределом функции , т.е.
.
Теорема доказана.
Теорема 2. Предел произведения конечного числа функций равен произведению пределов этих функций
.
Доказательство:
Не нарушая общности рассуждений, проведём доказательство для двух функций и .
Пусть 
, тогда , 
Найдём произведение функций и
Величина 
есть постоянная величина, 
бесконечно малая функция. Следовательно, число является пределом функции 
, то есть справедливо равенство
.
Следствие: 
.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля
.
Доказательство: Пусть 
, 
Тогда 
, 
.
Найдём частное 
и проделаем над ним некоторые тождественные преобразования
Величина 
постоянная, дробь 
бесконечно малая. Следовательно, функция представлена в виде суммы постоянного числа и бесконечно малой функции.
Тогда .
Замечание. Теоремы 1–3 доказаны для случая . Однако, они могут быть применимы при 
, поскольку доказательство теорем в этом случае проводится аналогично.
Например. Найти пределы:
1. 
;
2. 
;
3. 
;
4. 
. В этом пределе теорему о пределе частного непосредственно применять нельзя, т.к. предел знаменателя равен нулю. Поэтому сначала многочлен, стоящий в числителе разложим на множители, после этого сократим дробь и вычислим предел. 
;
5. 
;
6. 
. Теорему о пределе частного здесь применять нельзя, так как числитель и знаменатель конечного предела не имеют. В этом случае сначала числитель и знаменатель делят на степень 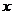с наивысшим показателем, а затем переходят к пределу: 
;
7. 
Если под знаком предела имеется иррациональность и предел знаменателя равен нулю, то необходимо перенести иррациональность в числитель, для чего домножить знаменатель и числитель на выражение, сопряженное знаменателю. 
