Предельные точки последовательности. (Два определения и их эквивалентность)

Определение 1. Число a называется предельной точкой последовательности { x _n}, если из последовательности { x _n} можно выделить подпоследовательность, сходящуюся к a.

Определение 2. Число a называется предельной точкой последовательности { x _n}, если в любой e-окрестности точки a содержится бесконечно много членов последовательности { x _n}.

Утверждение. Определения 1 и 2 эквивалентны.

В самом деле, пусть a - предельная точка последовательности { x _n} по первому определению, тогда существует подпоследовательность 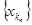® a, и в любой e-окрестности точки a содержится бесконечно много членов последовательности { x _n}, а это и означает, что точка a является предельной точкой последовательности по определению 2.

Пусть { x _n} - числовая последовательность, и пусть k ₁ , k ₂, …, k _n, … - возрастающая последовательность, элементами которой являются натуральные числа. Выберем из последовательности { x _n} элементы с номерами k ₁ , k ₂, …, k _n, …, получим вот такую последовательность: 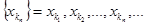, она называется подпоследовательностью последовательности { x _n}. Отметим, что k _n ³ n. Примеры подпоследовательностей:

1) { x _2n} = x ₂, x ₄, …, x _2n, …

2) 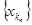= x ₁, x ₃, x ₇, x ₁₃, …

3) { x _n} - сама последовательность.