Критерий Коши сходимости последовательности

Определение: Последовательность { x _n} называется фундаментальной, если " e > 0 $ N, " n > N и " натурального p: ½ x _n+p- x _n½ < e.

Так как m = n + p - тоже произвольное число > N, то определение фундаментальности можно сформулировать следующим образом: " e > 0 $ N, " n > N и " m > N:½ x _m- x _n½ < e.

Геометрически фундаментальность последовательности { x _n} означает, что для любого сколь угодно малого e существует такой номер N, что любые два члена последовательности с большим, чем N, номерами, отстоят друг от друга не более, чем на e.

(здесь рисунок)

Пример: Докажем, что последовательность 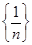=1, 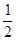, , 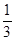… - фундаментальная. Зададим произвольное e > 0, возьмем N > 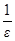. Тогда 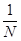> e, и " n > N и " натурального p: ½ x _n+p- x _n½ = 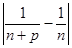= 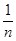- 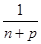< < 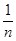< 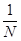e. Это и означает, что последовательность 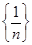- фундаментальная.

Лемма 2. Фундаментальная последовательность ограничена.

Доказательство: Пусть { x _n} - фундаментальная последовательность. Возьмем какое-нибудь положительное e, например, e = 1. По определению фундаментальности, $ N, " n > N и " m > N:½ x _m- x _n½ < 1. Зафиксируем какое-нибудь m ₀ > N, тогда 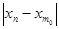< 1 при n > N, или 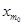- 1 < x _n < 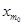+ 1 при n > N. Таким образом, все члены последовательности с номерами n > N лежат в интервале ( 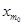- 1, 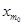+ 1), вне этого интервала лежит только конечное число членов последовательности. Это и означает, что последовательность { x _n} ограничена.

Лемма доказана.

Теорема 6.4 (критерий Коши сходимости последовательности) Для того, чтобы числовая последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.