2015-04-20
1128
Теорема 9.9. Пусть
- n ³ 1 – целое число
- функция 
имеет производную порядка n в некоторой окрестности точки с и производную порядка n + 1 в самой точке с
- справедливы следующие соотношения:
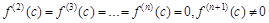(2)
Тогда, если n является четным числом, график функции имеет перегиб в точке M(c, f(c)). Если же n является нечетным числом и, кроме того,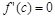 
, функция имеет локальный экстремум в точке с, точнее, локальный минимум при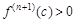 
и локальный максимум при 
.
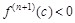Доказательство. (для случая экстремума)
Пусть n ³ 1 является нечетным числом и 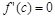. Т. к. при n = 1 теорема совпадает с Теоремой 9.2, то достаточно провести доказательство для нечетного n ³ 3. Для определенности проведем рассуждения для случая 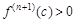. Для случая 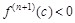они проводятся аналогично.
Из условия 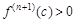и из Теоремы 8.9 ( Теорема 8.9. Если функция f (x) дифференцируема в точке с и 
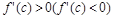, то эта функция возрастает (убывает) в точке с.), примененной к 
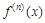вытекает, что эта функция возрастает в точке с. Т. к., кроме того, 
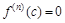, то это означает, что найдется достаточно малая окрестность точки с, в пределах которой 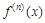отрицательна слева от с и положительна справа от с. Разложим f’ (x) в окрестности точки с в ряд Тейлора с остаточным членом в форме Лагранжа. Мы получим, что для всех x из достаточно малой окрестности точки с между с и x найдется точка x такая, что
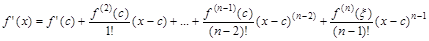(3)
Соотношения (2) и условие 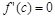позволяют переписать (3) в виде
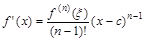(4)
Т. к. x всегда лежит между c и x, то для всех x из достаточно малой окрестности точки с производная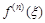 
отрицательна при 
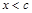и положительна при 
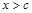. При нечетном n число n – 1 является четным, а поэтому вся правая (а, следовательно, и левая) часть (4) для всех x из достаточно малой окрестности с отрицательна слева от с и положительна справа от с.
На основании Теоремы 9.1 это означает, что функция f (x) имеет локальный минимум в точке с.
Случай 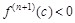рассматривается совершенно аналогично.
