1). Предположим, что функция f (x) дифференцируема в любой точке интервала 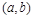 . Тогда существует касательная к графику функции
. Тогда существует касательная к графику функции  , проходящая через любую точку
, проходящая через любую точку 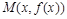 этого графика
этого графика 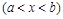 , причем эта касательная не параллельна оси Oy.
, причем эта касательная не параллельна оси Oy.
Определение. График функции  имеет на интервале
имеет на интервале 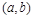 выпуклость, направленную вниз (вверх), если график этой функции в пределах указанного интервала лежит не ниже (не выше) любой своей касательной.
выпуклость, направленную вниз (вверх), если график этой функции в пределах указанного интервала лежит не ниже (не выше) любой своей касательной.
Теорема 9.4. Если функция  имеет на интервале
имеет на интервале 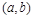 конечную вторую производную и если эта производная неотрицательна (неположительна) всюду на этом интервале, то график функции
конечную вторую производную и если эта производная неотрицательна (неположительна) всюду на этом интервале, то график функции  имеет на интервале
имеет на интервале 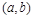 выпуклость, направленную вниз (вверх).
выпуклость, направленную вниз (вверх).
Доказательство. Рассмотрим случай 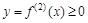 всюду на
всюду на 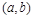 . Пусть с – любая точка интервала
. Пусть с – любая точка интервала 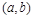 (рисунок). Требуется доказать, что график функции
(рисунок). Требуется доказать, что график функции  лежит не ниже касательной, проходящей
лежит не ниже касательной, проходящей
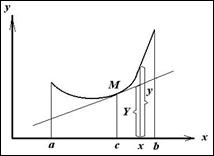
через точку 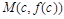 . Запишем уравнение касательной, обозначая ее ординату через Y. Т. к. угловой коэффициент касательной равен f’ (c), то
. Запишем уравнение касательной, обозначая ее ординату через Y. Т. к. угловой коэффициент касательной равен f’ (c), то
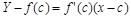 (1)
(1)
Разложим f (x) в окрестности точки с по формуле Тейлора до n = 1. Получим
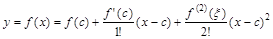 (2)
(2)
где остаточный член взят в форме Лагранжа, x лежит между c и x. Поскольку по условию f (x) имеет вторую производную на интервале 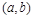 , формула (2) справедлива для любого x из этого интервала. Сопоставляя (2) и (1), имеем
, формула (2) справедлива для любого x из этого интервала. Сопоставляя (2) и (1), имеем
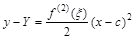 (3)
(3)
Поскольку вторая производная по условию ³ 0 всюду на 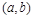 , то правая часть (3) неотрицательна, т.е. для всех x из
, то правая часть (3) неотрицательна, т.е. для всех x из 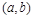
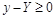 или
или 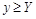 . Это неравенство доказывает, что график
. Это неравенство доказывает, что график  всюду в пределах интервала
всюду в пределах интервала 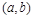 лежит не ниже касательной (1).
лежит не ниже касательной (1).
Аналогично доказывается теорема для случая 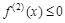 .
.
 2015-04-20
2015-04-20 537
537








