Определение. Точка 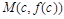 графика функции
графика функции  называется точкой перегиба этого графика, если существует такая окрестность точки с оси абсцисс, в пределах которой график функции
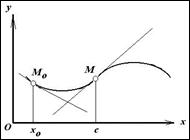
называется точкой перегиба этого графика, если существует такая окрестность точки с оси абсцисс, в пределах которой график функции  слева и справа от с имеет разные направления выпуклости. (см. рисунок).
слева и справа от с имеет разные направления выпуклости. (см. рисунок).
Иногда при определении точки перегиба графика функции  дополнительно требуют, чтобы этот график всюду в пределах достаточно малой окрестности точки с оси абсцисс слева и справа от с лежал по разные стороны от касательной к этому графику в точке
дополнительно требуют, чтобы этот график всюду в пределах достаточно малой окрестности точки с оси абсцисс слева и справа от с лежал по разные стороны от касательной к этому графику в точке 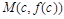 .
.
Лемма 1. Пусть функция  имеет производную f’ (x) всюду в d -окрестности точки с, причем эта производная непрерывна в точке с. Тогда, если график
имеет производную f’ (x) всюду в d -окрестности точки с, причем эта производная непрерывна в точке с. Тогда, если график  имеет на интервале
имеет на интервале 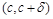 выпуклость, направленную вниз (вверх), то всюду в пределах интервала
выпуклость, направленную вниз (вверх), то всюду в пределах интервала 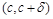 этот график лежит не ниже (не выше) касательной, проведенной в точке
этот график лежит не ниже (не выше) касательной, проведенной в точке 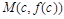 .
.
Доказательство. Рассмотрим последовательность 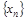 точек интервала
точек интервала 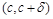 , сходящуюся к точке с. Через каждую точку
, сходящуюся к точке с. Через каждую точку 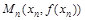 графика
графика  проведем касательную к этому графику, т.е. прямую
проведем касательную к этому графику, т.е. прямую
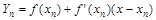
Т.к. по условию  имеет на интервале
имеет на интервале  выпуклость, напрвленную вниз (вверх), то для любого n и любой фиксированной точки x интервала
выпуклость, напрвленную вниз (вверх), то для любого n и любой фиксированной точки x интервала 
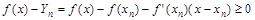 (£ 0) (1)
(£ 0) (1)
Из непрерывности f’ (x) в точке с следует, что существует предел
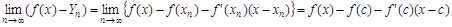 (2)
(2)
Из (2) и (1) следует, что
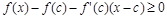 (£ 0) (3)
(£ 0) (3)
Если обозначить через Y текущую ординату касательной, проходящей через точку 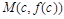 , то (3) можно переписать в виде
, то (3) можно переписать в виде
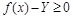 (£ 0) (4)
(£ 0) (4)
Переходя в неравенстве (1) к пределу при 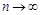 получим, что
получим, что
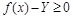 (£ 0) (5)
(£ 0) (5)
для любой фиксированной точки x из интервала 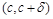 .
.
 2015-04-20
2015-04-20 440
440








