2015-04-20
382
Замечание. Для интервала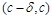 
доказательство аналогично.
Лемма 2. Пусть функция 
имеет производную f’ (x) в некоторой окрестности точки с, причем эта производная непрерывна в точке с.
Тогда, если график функции имеет перегиб в точке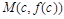 
, то в пределах достаточно малой d -окрестности точки с этот график слева и справа от с лежит по разные стороны от касательной, проведенной через точку .
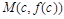Доказательство. Выберем d > 0 настолько малым, чтобы на каждом из интервалов 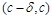и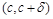 
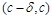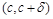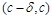график имел определенное направление выпуклости (различное на интервалах и ). Применяя Лемму 1 к функции по каждому из интервалов и 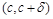докажем Лемму 2.
