Лемма 2 позволяет установить необходимое условие перегиба графика дважды дифференцируемой в данной точке функции.
Теорема 9.6. (необходимое условие перегиба графика функции). Если функция  имеет в точке с вторую производную и график этой функции имеет перегиб в точке
имеет в точке с вторую производную и график этой функции имеет перегиб в точке 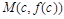 , то
, то 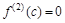 .
.
Доказательство. Пусть Y – текущая координата касательной 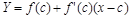 , проходящей через точку
, проходящей через точку 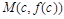 . Рассмотрим функцию
. Рассмотрим функцию
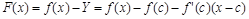 ,
,
равную разности f (x) и линейной функции 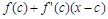 . Эта функция, как и функция f (x) имеет в точке с вторую производную. По Лемме 2 в малой окрестности точки с график
. Эта функция, как и функция f (x) имеет в точке с вторую производную. По Лемме 2 в малой окрестности точки с график  лежит слева и справа от с по разные стороны от касательной, проходящей через точку
лежит слева и справа от с по разные стороны от касательной, проходящей через точку 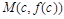 , следовательно, функция F (x) в малой окрестности точки с имеет слева и справа от нее разные знаки.
, следовательно, функция F (x) в малой окрестности точки с имеет слева и справа от нее разные знаки.
Стало быть, функция F (x) не может иметь в точке с локального экстремума.
Предположим теперь, что 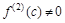 . Тогда, поскольку
. Тогда, поскольку 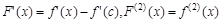 , выполняются условия
, выполняются условия 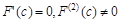 и функция в силу Теоремы 9.2 имеет в точке с локальный экстремум. Полученное противоречие доказывает, что предположение
и функция в силу Теоремы 9.2 имеет в точке с локальный экстремум. Полученное противоречие доказывает, что предположение 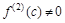 является неверным, т.е.
является неверным, т.е. 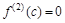 .
.
|
|
|
 2015-04-20
2015-04-20 326
326








