2015-04-23
2538
Приложение 2.
Системы и совокупности уравнений. Методы их решения
Уравнения с двумя переменными
Многие теоретические и практические вопросы приводят к уравнению с несколькими неизвестными или к целой системе уравнений с несколькими неизвестными.
Определение. Пусть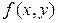 
– выражение с двумя переменными определенное на множестве 
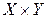. Равенство вида 
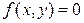, определенное на множестве 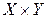, называют уравнением с двумя переменными.
Областью определения уравнения с двумя переменными является множество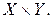 
Упорядоченную пару значений переменных обращающую уравнение с двумя переменными в верное числовое равенство, называют решением уравнения с двумя переменными.
Пример. Решениями уравнения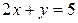 
являются пары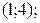 
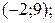(2;1). Это уравнение имеет и другие решения.
Для нахождения решений уравнения 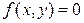удобно выразить одну переменную через другую, например, 
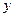через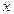 
.
Пример. Для нахождения решений уравнения 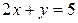выражают одну переменную через другую, например, 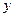через 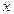, получают уравнение 
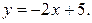Выбрав произвольное значение 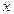, вычисляют соответствующее значение .
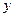Если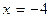 
, то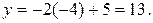 
Следовательно, пара 
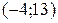является решением данного уравнения; если 
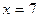, то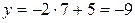 
, значит, пара 
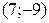так же является решением заданного уравнения и т.д.
Множество всех решений уравнения 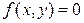называют множеством решений уравнения.
Как правило, уравнения с двумя переменными имеют бесконечное множество решений. Его удобно изображать на координатной плоскости, где все решения уравнения изображают точками на координатной плоскости и получают некоторое множество точек, которые называют графиком уравнения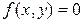 
.
Так, графиком уравнения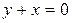 
является прямая 
; графиком уравнения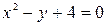 
является парабола 
.
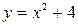Уравнениями с двумя переменными являются уравнения вида:
o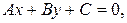 
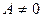, В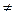 
0 – общее уравнение прямой;
o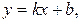 
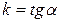– угловой коэффициент, равный тангенсу угла наклона прямой к оси 
, 
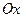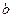– ордината точки пересечения прямой с осью 
;
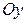o уравнение окружности вида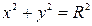 
с центром в начале координат и радиусом 
;
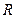o уравнение окружности с центром в точке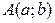 
и радиусом 
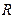имеет вид: 
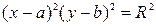и др.
Для уравнений с двумя переменными справедливы утверждения аналогичные утверждениям для уравнений с одной переменной.
