Систему уравнений с несколькими неизвестными наиболее часто решают:
− методом подстановки;
− методом сложения;
− графическим методом;
− методом введения новых переменных.
При решении системы методом подстановки пользуясь одним уравнением системы, выражают одну из переменных системы через другие переменные, и заменяют в остальных уравнениях эту переменную полученным выражением. При этом получают систему уравнений равносильную данной системе.
Уравнение 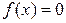 приводят к виду
приводят к виду 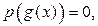 вводят новую переменную
вводят новую переменную 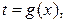 решают уравнение
решают уравнение 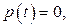 затем решают совокупность уравнений
затем решают совокупность уравнений 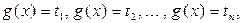 , где
, где 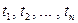 – корни уравнения
– корни уравнения 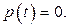
Решим систему двух линейных уравнений с двумя неизвестными 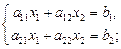 где
где 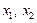 – неизвестные;
– неизвестные; 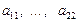 – коэффициенты при неизвестных,
– коэффициенты при неизвестных, 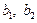 – свободные члены, в общем виде.
– свободные члены, в общем виде.
Из одного уравнения выразим одно из неизвестных, например 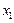 , через коэффициенты и другое неизвестное
, через коэффициенты и другое неизвестное 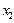 :
: 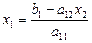 и подставим во второе уравнение вместо
и подставим во второе уравнение вместо 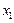 :
: 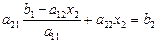 .
.
Решая последнее уравнение, находим 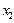 :
:
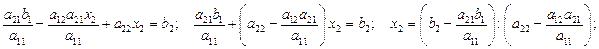
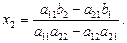
Подставим это значение вместо 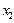 в выражение
в выражение 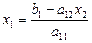 :
:
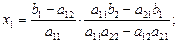
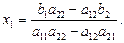
Таким образом, способ подстановки решения системы двух уравнений с двумя неизвестными заключается в следующем:
− выражают одну переменную через другую в одном из уравнений системы;
− это выражение подставляют в другое уравнение системы, и в результате получают уравнение с одной переменной;
− в уравнении с одной переменной находят корень;
− подставив найденный корень, получают значение другой переменной;
− записывают ответ.
Пример. Решим систему методом подстановки: 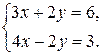
Решение. Из первого уравнения системы 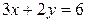 выразим переменную
выразим переменную 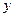 через
через 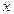 , получим
, получим 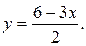 Подставив это выражение во второе уравнение системы, имеем:
Подставив это выражение во второе уравнение системы, имеем: 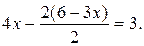
Система уравнений 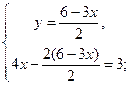 равносильна системе
равносильна системе 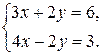 Из уравнения
Из уравнения 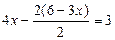 найдем
найдем 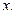
Отсюда, 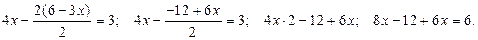
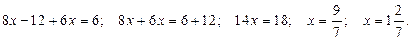
Подставив теперь найденное значение 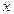 в выражение
в выражение 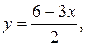 получим:
получим: 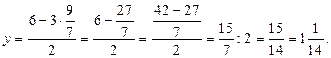
Ответ. 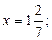
Пример. Решим систему методом подстановки: 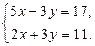
Решение. Из второго уравнения системы выразим 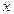 через
через 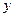 , получим
, получим 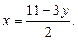 Подставив это выражение в первое уравнение системы, имеем:
Подставив это выражение в первое уравнение системы, имеем: 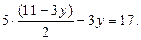 Из данного уравнения найдем
Из данного уравнения найдем 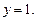 Подставив
Подставив 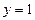 в выражение
в выражение 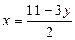 , найдем
, найдем 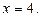 Решение системы: (4;1).
Решение системы: (4;1).
Ответ. (4;1).
Метод алгебраического сложения (вычитания).
Решим систему двух уравнений с двумя неизвестными 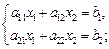 где
где 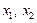 – неизвестные;
– неизвестные; 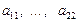 – коэффициенты при неизвестных,
– коэффициенты при неизвестных, 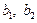 – свободные члены, методом алгебраического сложения в общем виде.
– свободные члены, методом алгебраического сложения в общем виде.
Умножим обе части 1-го уравнения системы на (– 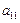 ), а обе части 2-го уравнения на
), а обе части 2-го уравнения на 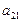 и сложим их:
и сложим их:
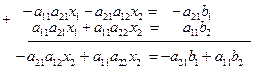
Отсюда получим: 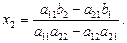
Подставим найденное значение вместо 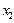 в любое уравнение системы
в любое уравнение системы 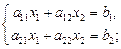 находим второе неизвестное:
находим второе неизвестное: 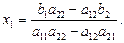
Таким образом, метод алгебраического сложения (вычитания) заключается в следующем:
− почленно складывают уравнения системы, предварительно умножив их на некоторые множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
− находят корень полученного уравнения с одной переменной;
− подставляют найденное значение в любое уравнение системы и находят соответствующее значение другой переменной;
− записывают ответ.
Пример. Решим систему уравнений: 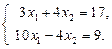
Решение. Решим систему способом сложения:
. 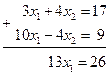
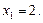
Подставим значение переменной 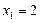 в первое (или второе) уравнение системы:
в первое (или второе) уравнение системы: 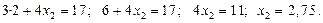
Пара (2; 2, 75) – решение системы.
Ответ. (2; 2,75).
Пример. Решим систему уравнений способом сложения: 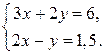
Решение. Решим систему способом сложения. Для этого умножим второе уравнение системы на 2 и сложим почленно уравнения системы:
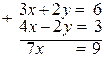
Найдем значения переменной 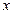 ,
, 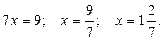 Найдем значения переменной
Найдем значения переменной 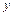 , для этого найденное значение
, для этого найденное значение 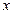 подставим в любое уравнение исходной (первоначальной) системы, получим:
подставим в любое уравнение исходной (первоначальной) системы, получим: 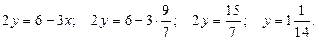 Ответ.
Ответ. 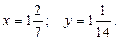
 2015-04-23
2015-04-23 6626
6626
