Графический метод решения систем уравнений

Графическое представление функций позволяет приближённо решать уравнения с одной или несколькими неизвестным, системы уравнений с двумя неизвестными.

Чтобы решить систему двух уравнений с двумя неизвестным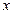и и 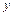, рассматривают каждое из уравнений как функциональную зависимость между переменным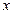и и 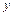, и строят графики этих функций. Координаты точек пересечения этих графиков дают нам искомые значения неизвестных 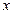и 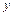, то есть решение этой системы уравнений.

Для того чтобы графически решить систему двух уравнений с двумя переменными, нужно в одной системе координат построить графики уравнений и найти координаты точек пересечения графиков.

Пример. Решим графически систему уравнений: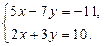

Решение. Построим в одной системе координат графики данных уравнений и найдем координаты точек пересечения полученных графиков. Графиками данных уравнений являются прямые, представленные на рисунке 5. В соответствии с графиками решением системы являются координаты точки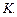

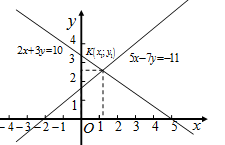Рис.5

Пример. Решим графически систему уравнений: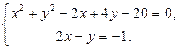

Решение. Выделяя полные квадраты, получаем:

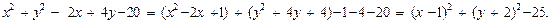
Следовательно, исходная система уравнений равносильна системе:

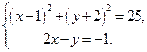
Графиком первого уравнения 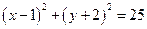является окружность с центром 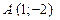и радиусом 5. Графики уравнений представлены на рисунке 6.

Графиком второго уравнения 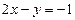является уравнение прямой, проходящей через точк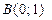и и 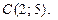Строим окружность радиуса 5 с центром в точке 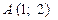и проводим прямую через точк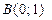и и 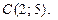Эти линии пересекаются в двух точках 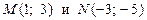. Значит решение системы: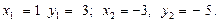

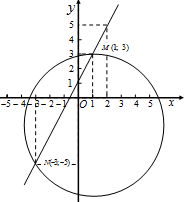Рис.6

Ответ. ;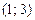

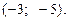
Пример. Решим графически систему уравнений: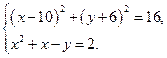

Решение. Построим в одной системе координат графики уравнений и найдем координаты точек пересечения этих графиков. Построим на координатной плоскости окружность с центром в точке 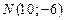и 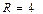и параболу у = х²+х–2 свершиной в точке 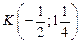иточками пересечения графика функции и оси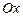 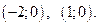Графики уравнений представлены на рисунке 7. Видим, что окружность и парабола не пересекаются, следовательно, система не имеет решений.

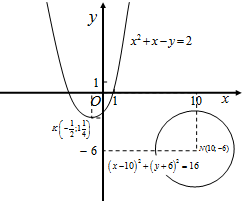Рис.7

Ответ. Система не имеет решений.