1. Упростите выражения с переменной:
1) 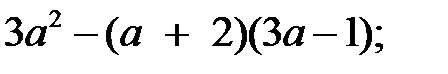 2)
2) 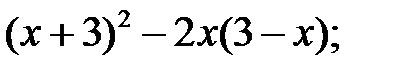
3) 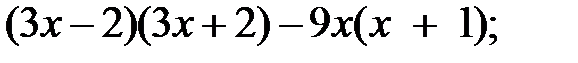 4)
4) 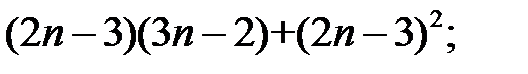
5) 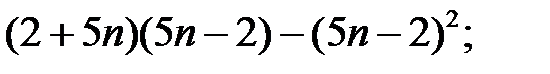 6)
6) 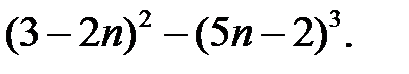
2. Преобразуйте в многочлен выражения с переменной:
1) 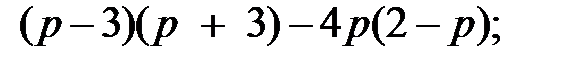 2)
2) 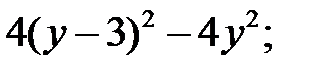 3)
3) 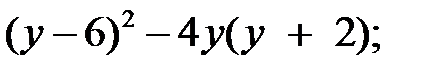
4) 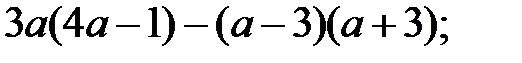 5)
5) 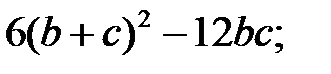 6)
6) 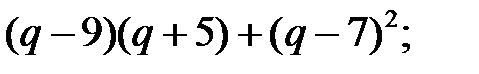
7) 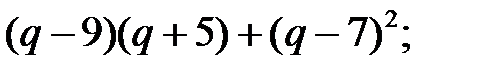 8)
8) 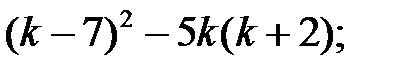 9)
9) 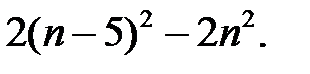
3. Разложите на множители выражения с переменными:
1) 49 p – p 3; 2) 2 c 2+8 bc +8 b 2; 3) 3 а 2–18 ab +27 b 2;
4) c 3–36 c; 5) 2 а 2–12 ab +18 b 2; 6) 7 а 2–28 a +28;
7) а 2+6 ab +9 b 2– c 2; 8) 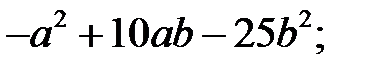 9)
9) 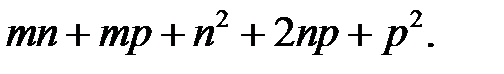
4. Представьте выражения с переменными в виде произведения:
1) 9– x 2–2 xy – y 2; 2) m 2–4 mn +4 n 2– m +2 n;
3) 1– а 2+10 ab –25 b 2; 4) m 2+2 mn + n 2– mp – np.
5. Разложите выражения с переменными на множители:
1) 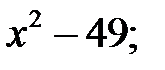 2)
2) 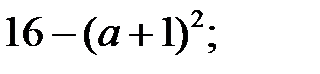 3)
3) 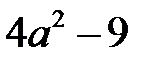 ;
;
4) c 3–8; 5) 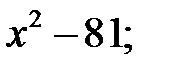 6)
6) 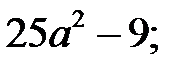
7) 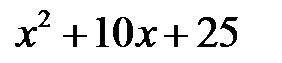 ; 8)
; 8) 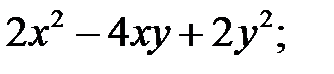 9)
9) 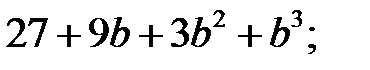
10) 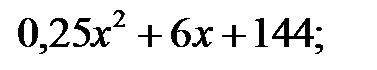 ; 1)
; 1) 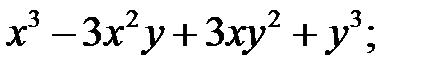 12)
12) 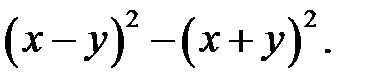
6. Разложите на множители квадратный трехчлен:
1) 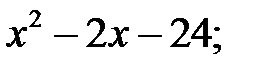 2)
2) 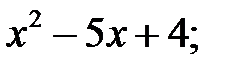 3)
3) 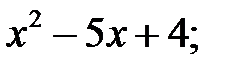
4) 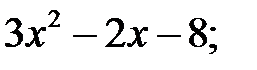 5) 2 а 2–12 a +18; 6)
5) 2 а 2–12 a +18; 6) 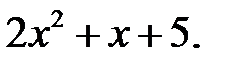
7. Докажите следующие тождества:
1) 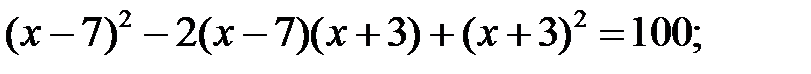
2) 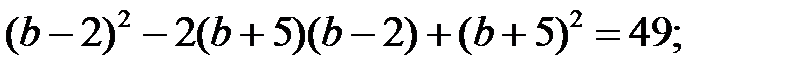
3) 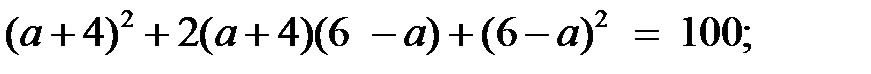
4) 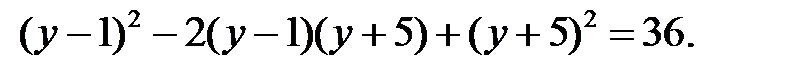
8. Упростите выражение 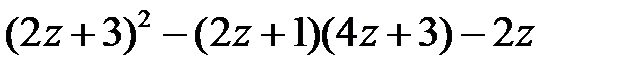 и найдите его значение при
и найдите его значение при 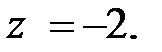
9. Упростите выражение 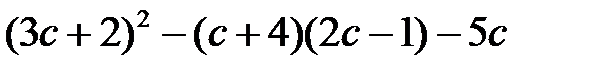 и найдите его значение при
и найдите его значение при 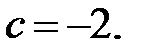
10. Упростите выражение 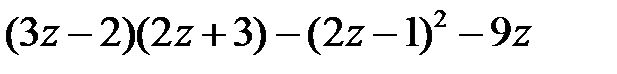 найдите его значение при
найдите его значение при 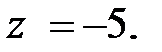
11 Сократите алгебраические дроби:
1) 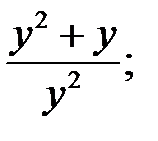 2)
2) 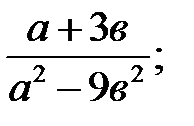 3)
3) 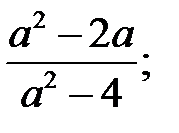 4)
4) 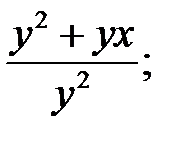 5)
5) 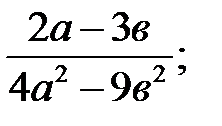 6)
6) 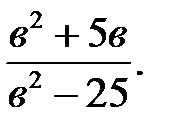
11. Выполните указанные действия:
1) 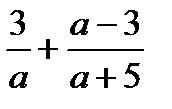 ; 2)
; 2) 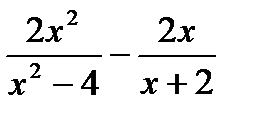 ; 3)
; 3) 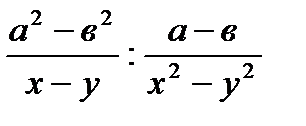
4) 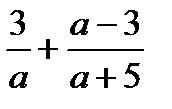 3; 5)
3; 5) 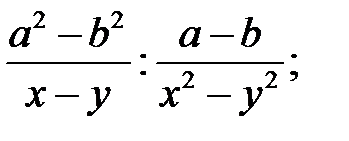 6)
6) 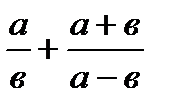 ;
;
7) 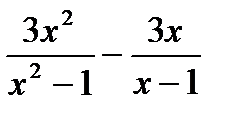 ; 8)
; 8) 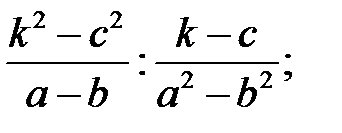 9)
9) 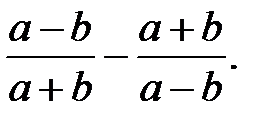
12. Упроститe выражения:
1) 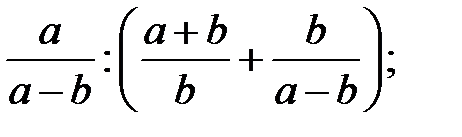 2)
2) 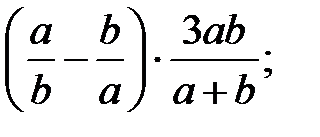 3)
3) 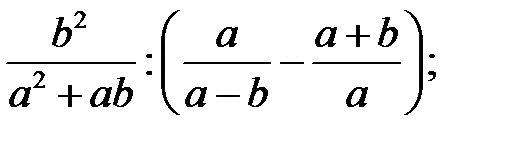
4) 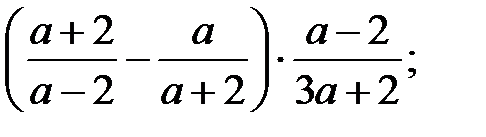 5)
5) 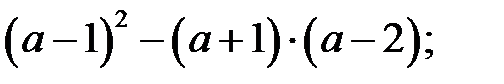 6)
6) 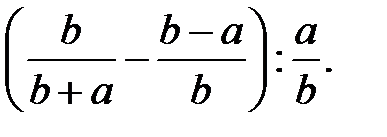
13. Упростите выражения:
1) 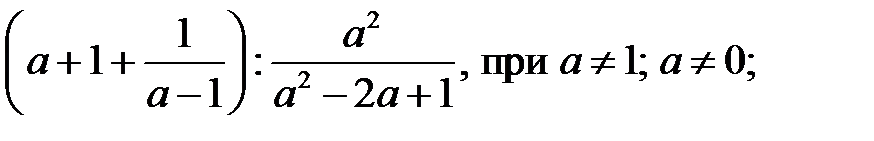 2)
2) 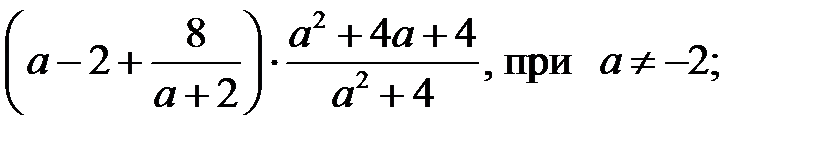
3) 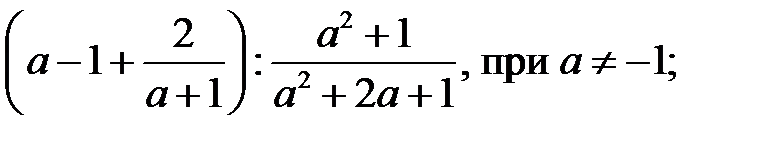 4)
4) 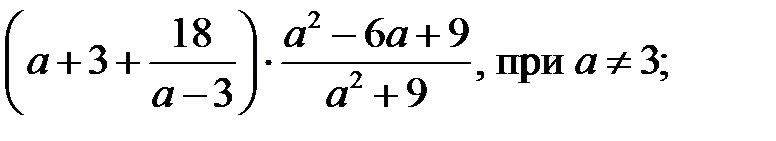
5) 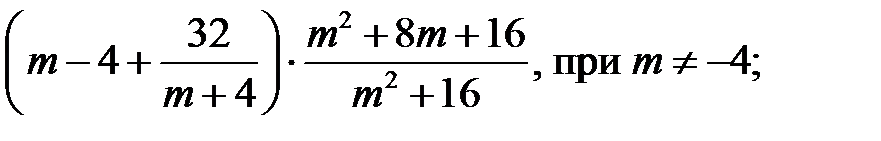
6) 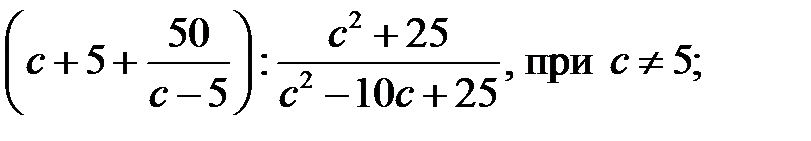 7)
7) 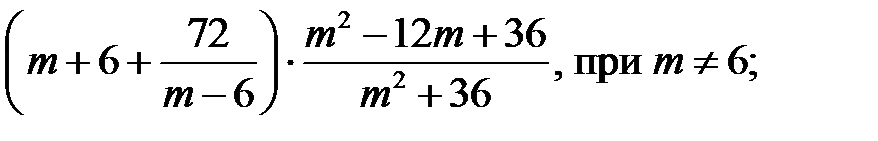
8) 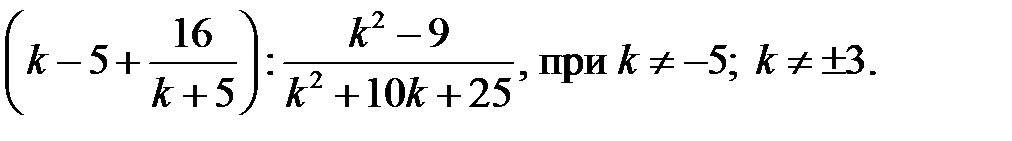
14. Упростить выражение: 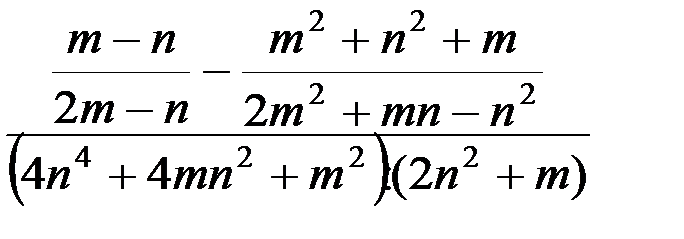 .
.
15. Упростить выражение: 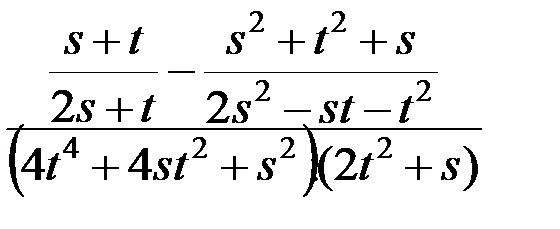 .
.
16. Найти область допустимых значений: 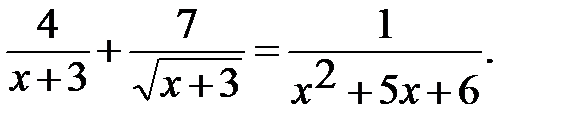
17. Являются ли уравнения равносильными:
1) 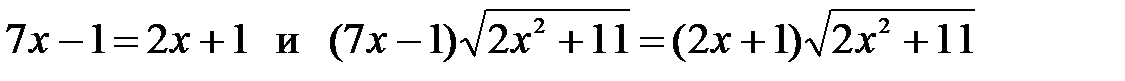 ;
;
2) 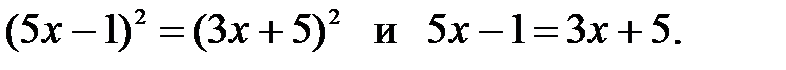
18. Привести пример, когда уравнения вида 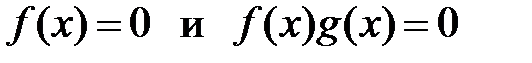
1) равносильны;
2) первое уравнение является следствием второго;
3) второе уравнение является следствием первое;
19. Найти область допустимых значений уравнения:
1) 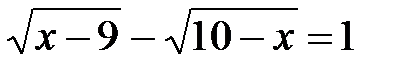 ;
;
2) 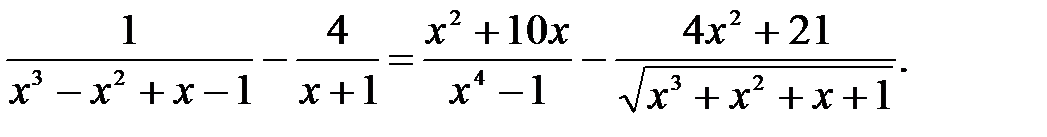
20. Являются ли равносильными уравнения:
1) 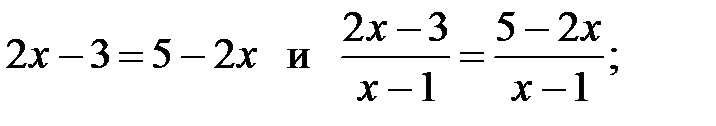
2) 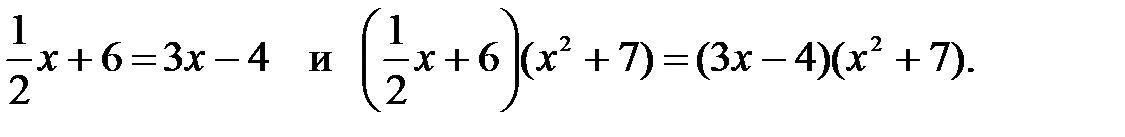
21. Какое из уравнений 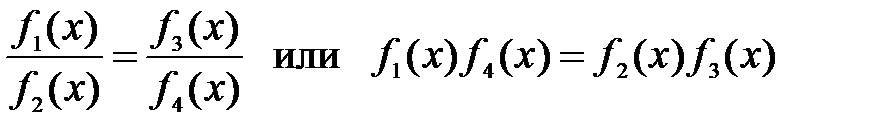
22. Какое из двух уравнений является следствием другого:
1) 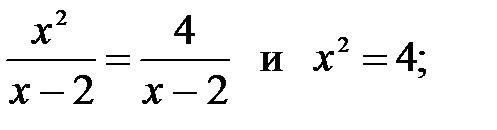
2) 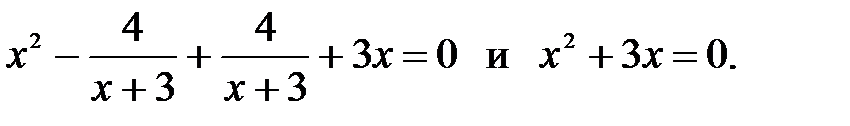
23. Какое из двух уравнений является следствием другого:
1) 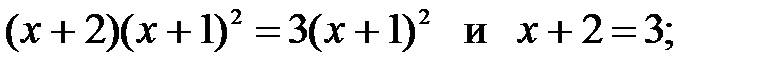
2) 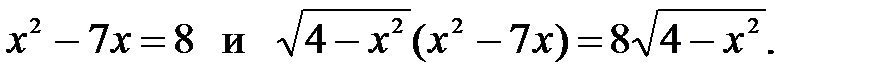
24. Равносильны ли два уравнения:
1) 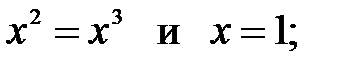
2) 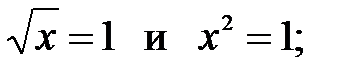
3) 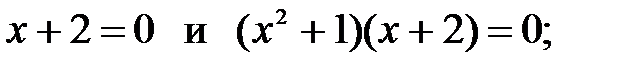
4) 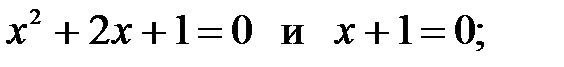
5) 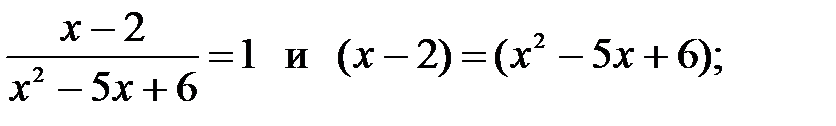
6) 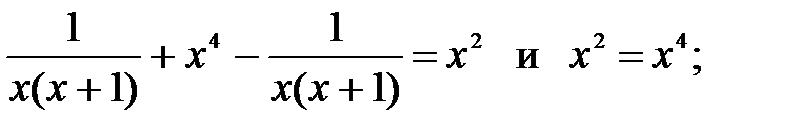
7) 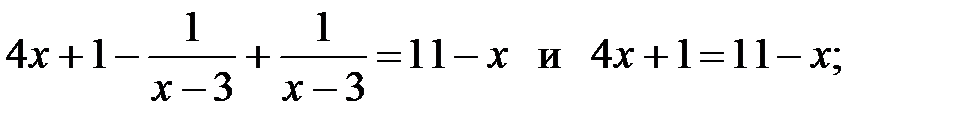
8) 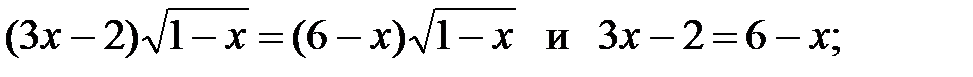
9) 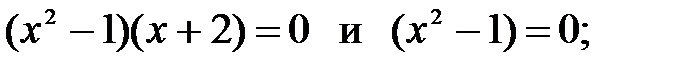
10) 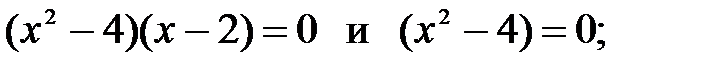
11) 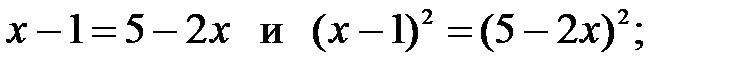
12) 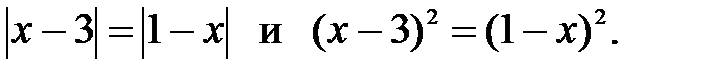
25. Равносильны ли два уравнения на множестве целых чисел:
1) 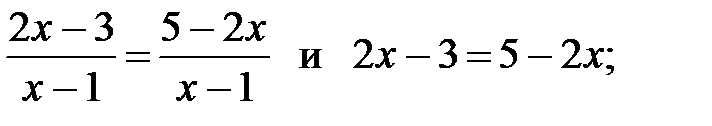
2) 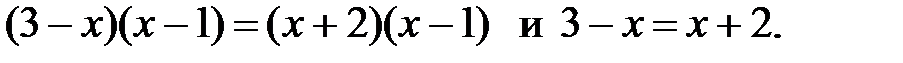
26. Равносильны ли следующие уравнения на множестве рациональных чисел:
1) 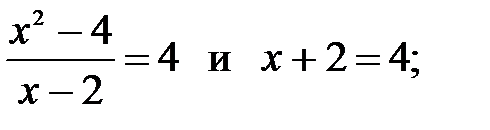
2) 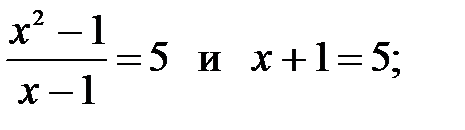
3) 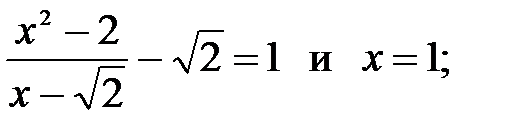
4) 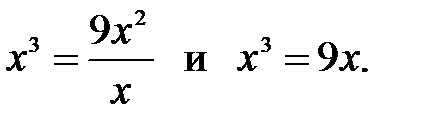
27. Выясните, равносильны ли на множестве всех действительных чисел данные уравнения:
1) 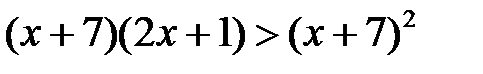 и
и 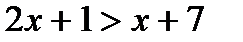 ;
;
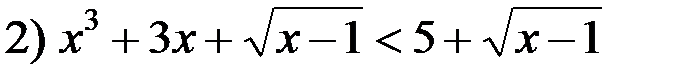 и
и 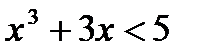 ;
;
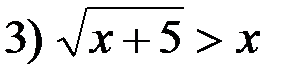 и
и 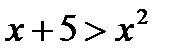 ;
;
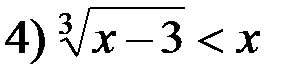 и
и 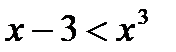 ;
;
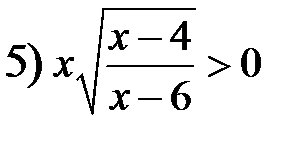 и
и 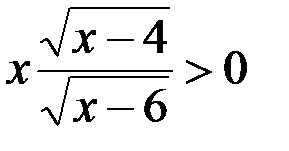 ;
;
6) 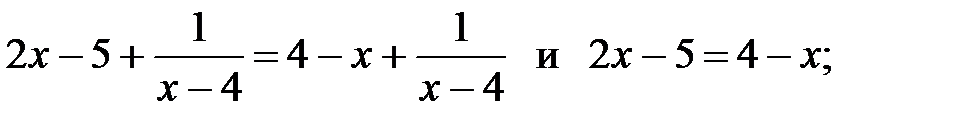
7) 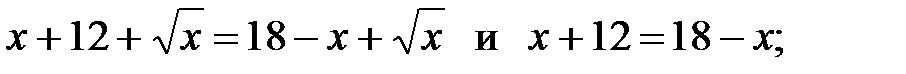
8) 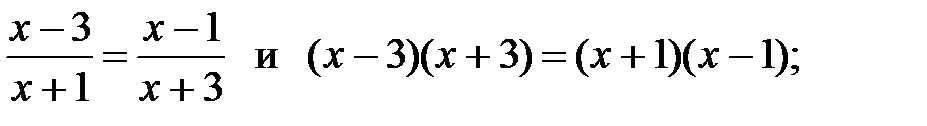
9) 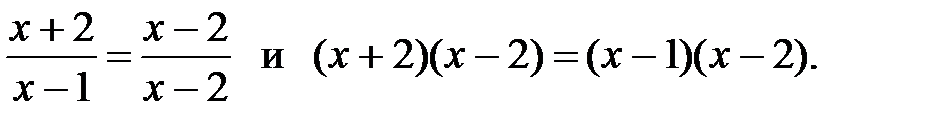
28. Решите уравнения:
1) 3 х –(5 х +4)=8; 2) 6 х –12=3+ х; 3) 8 х +2=3 х –18;
4) 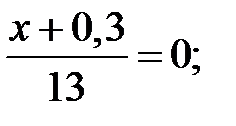 5) 2 х –(1+9 х)=20; 6) 4(2 у –3)=11–(2 у +13);
5) 2 х –(1+9 х)=20; 6) 4(2 у –3)=11–(2 у +13);
7) 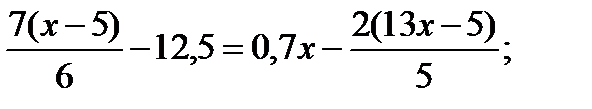 8)
8) 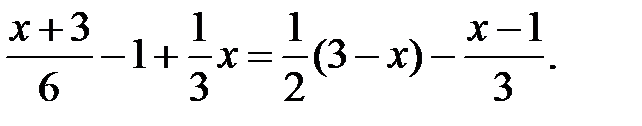
29. Укажите, при каких значениях параметра 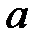 уравнение имеет бесконечно много решений:
уравнение имеет бесконечно много решений: 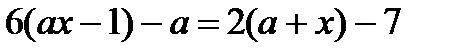 .
.
30. Выясните, при каких значениях параметра 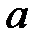 уравнение не имеет решений:
уравнение не имеет решений: 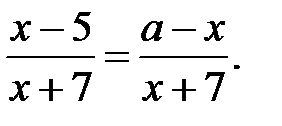
31. Решите квадратные уравнения:
1) 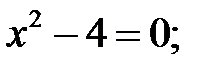 2)
2) 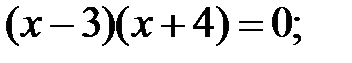 3)
3) 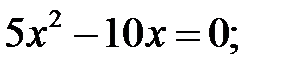
4) 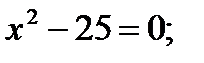 5)
5) 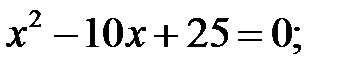 6)
6) 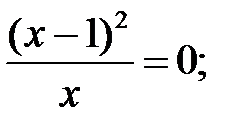
7) 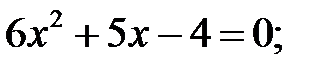 8)
8) 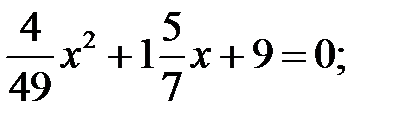 9)
9) 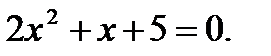
32. Решите квадратные уравнения с помощью теоремы Виета:
1) 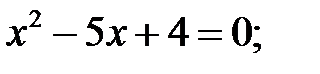 2)
2) 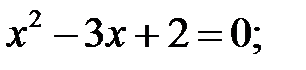 3)
3) 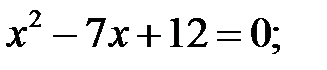
4) 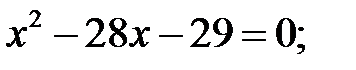 5)
5) 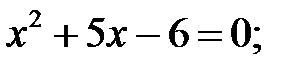 6)
6) 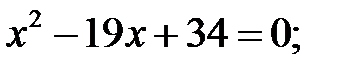
7) 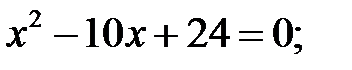 8)
8) 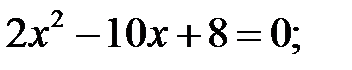 9)
9) 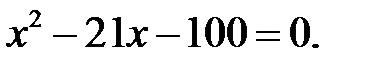
33. При каких значения параметра 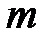 , уравнение
, уравнение 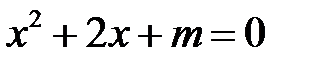 имеет два различных корня?
имеет два различных корня?
34. Найдите все целые значения параметра 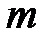 , при которых уравнение имеет два корня:
, при которых уравнение имеет два корня: 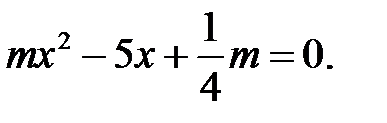
35. Определите, при каких значениях параметра 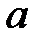 один из корней уравнения
один из корней уравнения 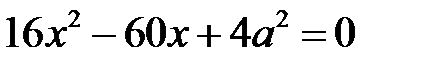 является квадратом другого.
является квадратом другого.
36. При каких значениях параметра 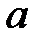 уравнение
уравнение 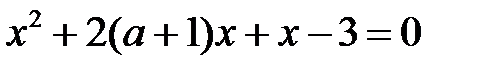 имеет корни разных знаков, которые не превосходят числа 5?
имеет корни разных знаков, которые не превосходят числа 5?
37. Решите биквадратные уравнения:
1) 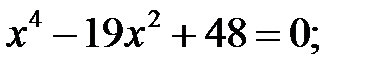 2)
2) 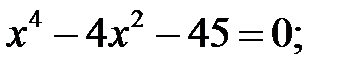 3)
3) 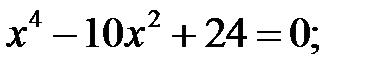 4)
4) 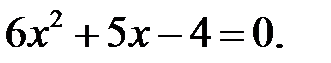
38. Решите уравнения:
1) 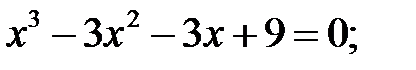 2)
2) 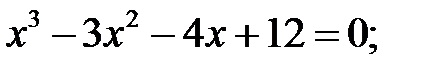
3) 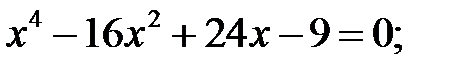 4)
4) 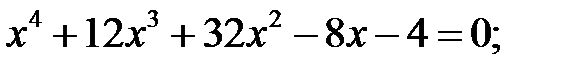
5) 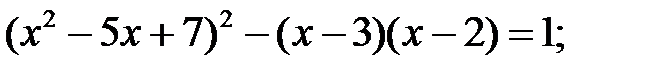 6)
6) 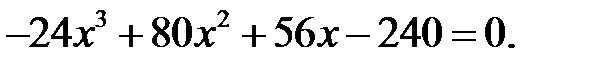
7) 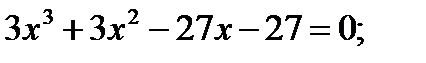 8)
8) 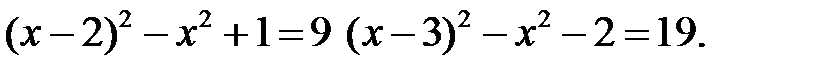
39. Решите уравнения:
1) 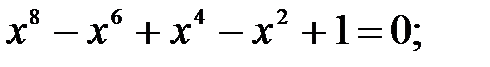 2)
2) 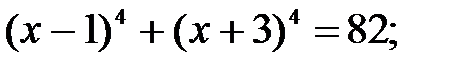
3) 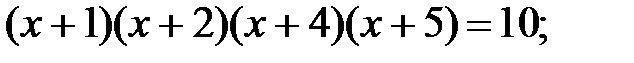 4)
4) 
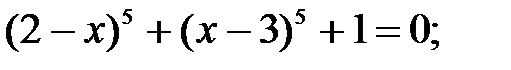
5) 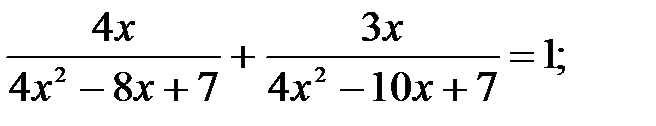 6)
6) 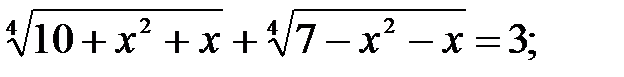
7) 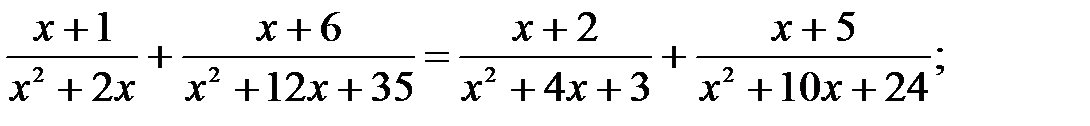
8) 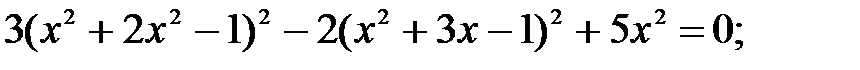
9) 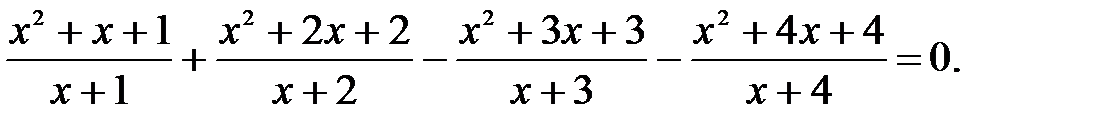
40. Решите уравнения:
1) 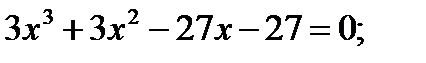 2)
2) 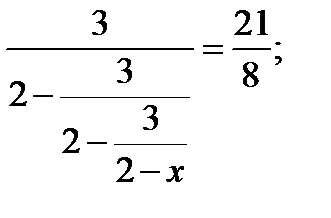
3) 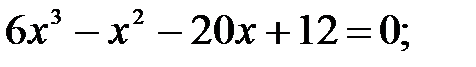 4)
4) 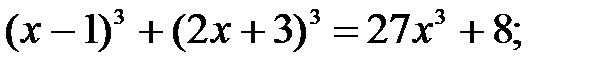
5) 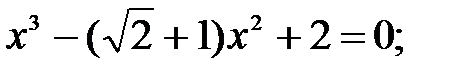 6)
6) 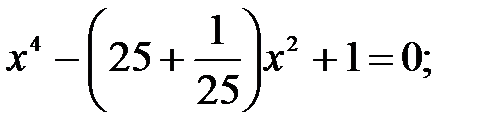
7) 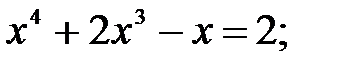 8)
8) 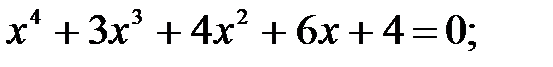
9) 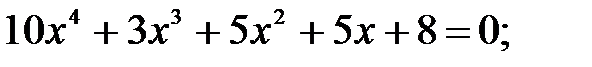 10)
10) 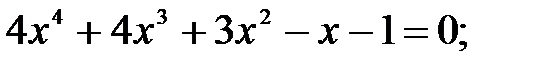
11) 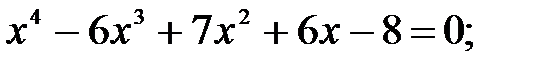 12)
12) 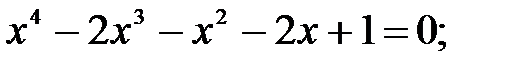
13) 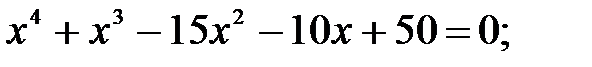 14)
14) 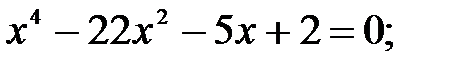
15) 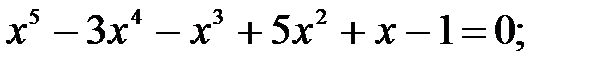 16)
16) 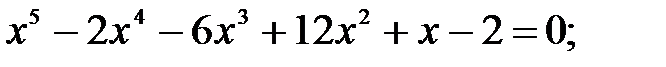
17) 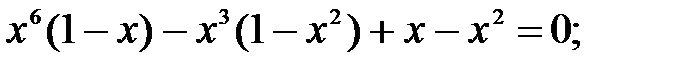 18)
18) 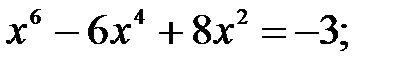
19) 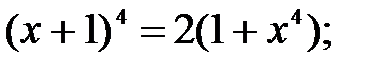 20)
20) 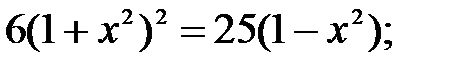
21) 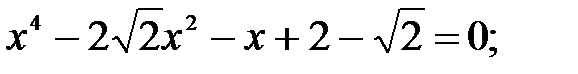 22)
22) 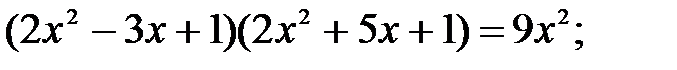
23) 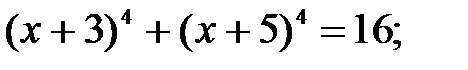 24)
24) 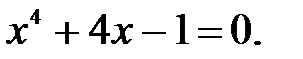
41. Проведите деление многочлена на многочлен с остатком.
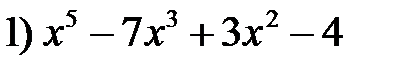 на
на 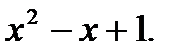
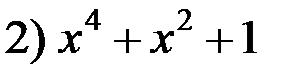 на
на 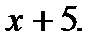
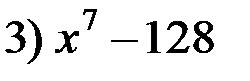 на
на 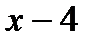 .
.
42. При каком значении параметра 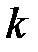 выполняется деление многочлена
выполняется деление многочлена 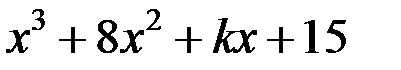 на многочлен
на многочлен 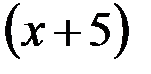 без остатка?
без остатка?
43. Сократите алгебраические дроби:
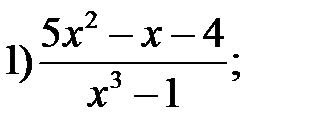
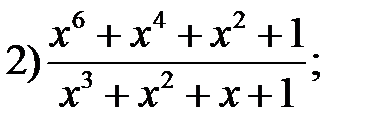
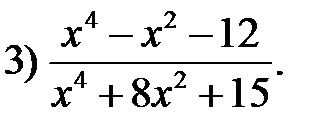
44. Решите уравнения методом введения новой переменной:
1) 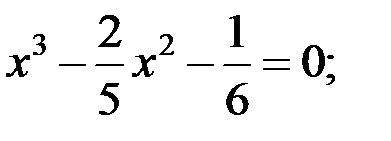 2)
2) 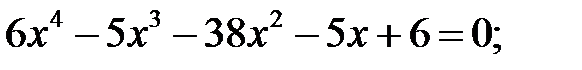
3) 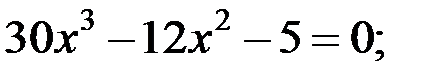 4)
4) 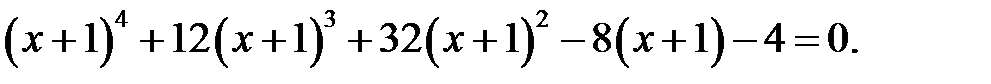
45. Найдите корни уравнения:
1) 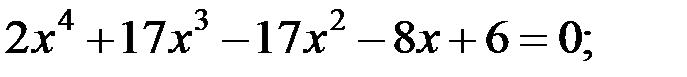 2)
2) 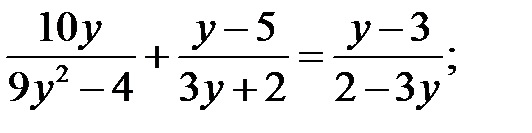
3) 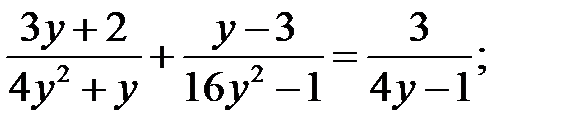 4)
4) 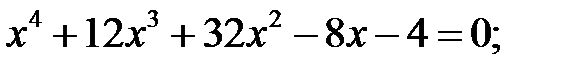
5) 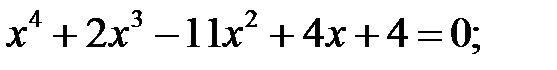 6)
6) 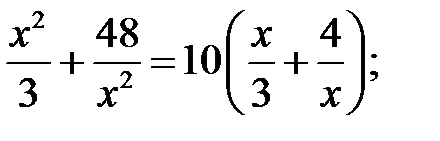
7) 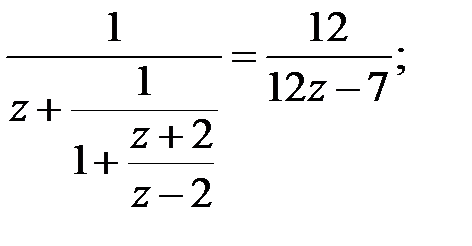 8)
8) 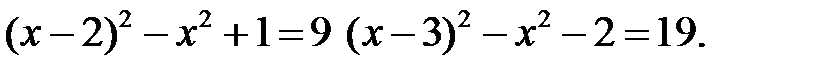
46. Найдите корни уравнения: 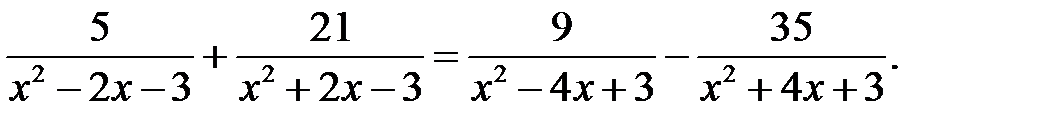
Указание. Примените подстановку 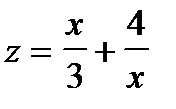 .
.
47. Решите уравнения:
1) 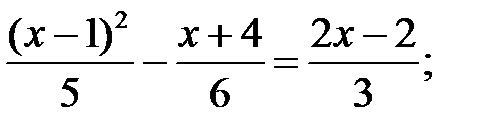 2)
2) 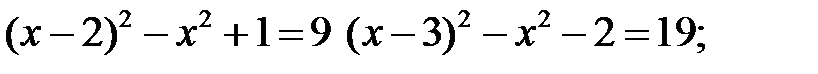
3) 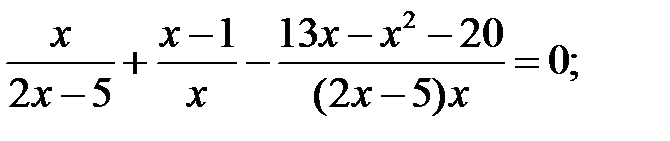
4) 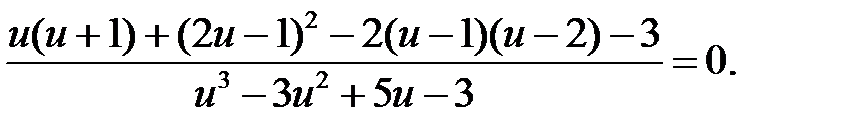
48. Найти все целочисленные решения уравнения 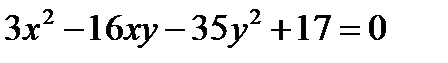 .
.
49. Найдите корни уравнения:
1) 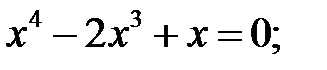 2)
2) 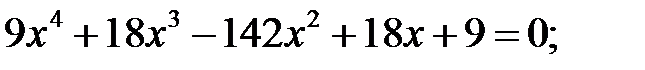
3) 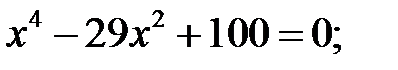 4)
4) 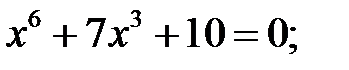
5) 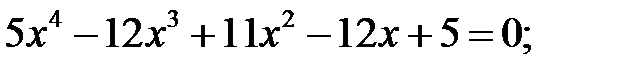 6)
6) 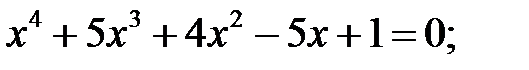
7) 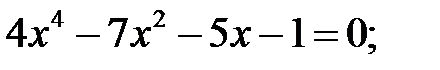 8)
8) 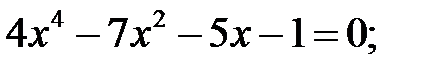
9) 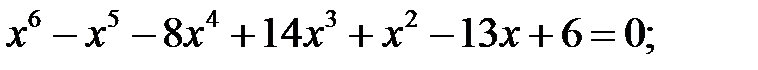
50. Решите уравнения:
1) 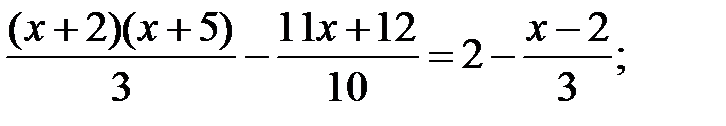 2)
2) 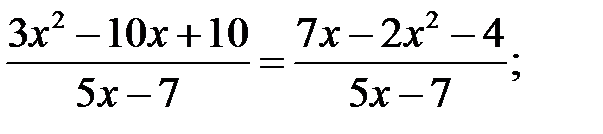
3) 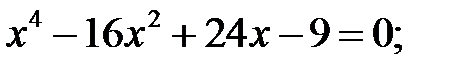 4)
4) 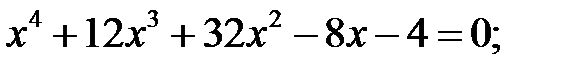
5) 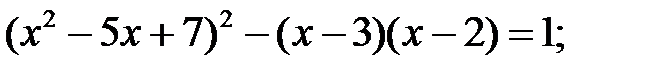 6)
6) 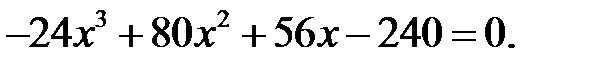
7) 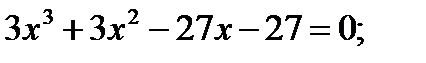 8)
8) 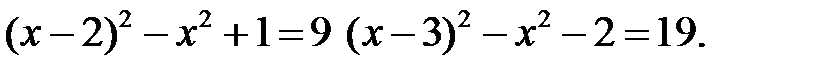
9) 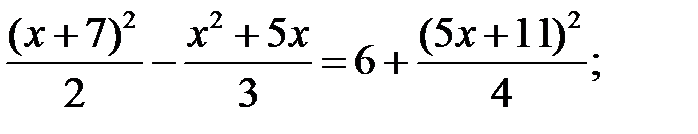 10)
10) 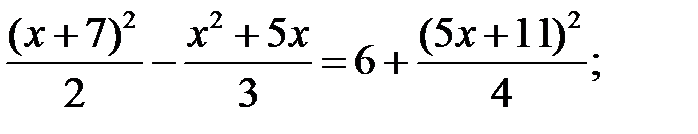
11) 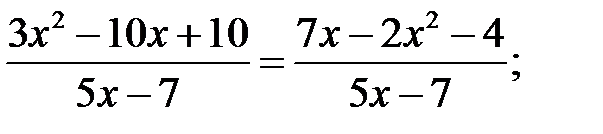 12)
12) 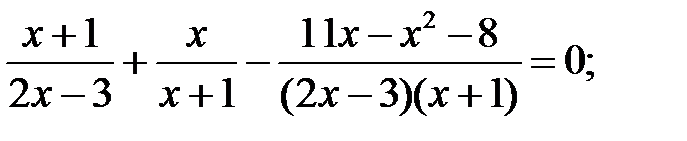
13) 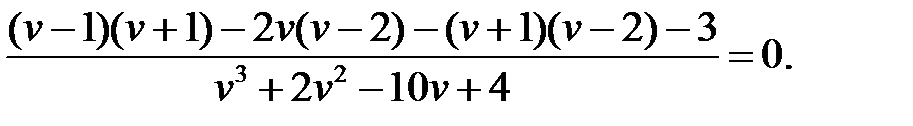
 2015-04-23
2015-04-23 655
655








