Удачный выбор новой переменной делает структуру уравнения более прозрачной. Новая переменная иногда очевидна, иногда несколько завуалирована, но «ощущается», а иногда «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы.
В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ситуациях.
Сначала остановимся на случаях, где замена очевидна.
Пример. Решим иррациональное уравнение: 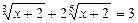
Решение. Введем новую переменную. Пусть 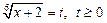 ,
, 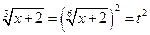 , тогда:
, тогда: 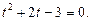
По теореме, обратной теореме Виета, имеем: 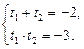
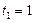 и
и 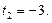
Но 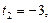
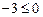 , следовательно,
, следовательно, 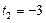 не удовлетворяет условию:
не удовлетворяет условию: 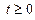 .
.
Возвращаясь к исходной переменной, имеем:
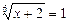
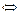
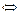
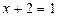
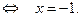
Ответ. 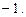
Пример. Решим уравнение: 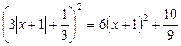 .
.
Решение. Введем новую переменную. Пусть 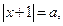 тогда:
тогда: 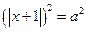 .
.
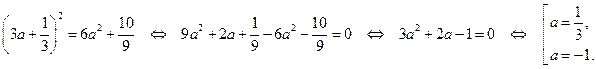
Возвращаясь к исходной переменной, имеем: 
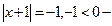 корней нет,
корней нет,
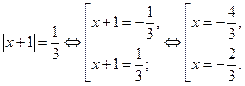
Ответ. 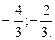
Пример. Решим уравнение: 7 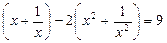 .
.
Решение. Введем новую переменную. Пусть 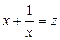 , тогда:
, тогда: 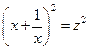 ,
,
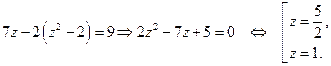
Возвращаясь к исходной переменной, имеем:
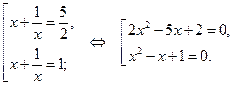
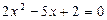 , или
, или 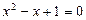 ,
,
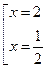 или
или 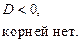
Ответ. 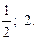
Пример. Решим уравнение: 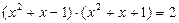 .
.
Решение. Попытка перемножить скобки в левой части исходного уравнения приведёт к уравнению четвёртой степени, решение которого требует трудоёмких вычислений.
Введем новую переменную. Пусть: 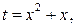 тогда:
тогда: 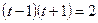 .
.
Раскрыв скобки, получим: 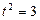
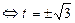 .
.
Возвращаясь к исходной переменной, имеем: 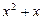 =
= 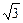 или
или 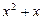 = -
= - 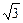 .
.
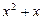
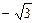 =
= 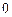 или
или 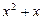
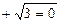 .
.
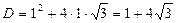 или
или 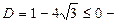 корней нет.
корней нет.
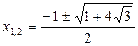 . Ответ.
. Ответ. 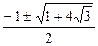 .
.
В примерах, приведенных выше замена очевидна. Однако во многих случаях удобная замена далеко не так очевидна, и поэтому необходимо выполнить некоторые преобразования. Тем самым выявим возможность применения метода замены неизвестного в нестандартных ситуациях.
Пример. Решим уравнение: 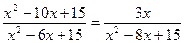 .
.
Решение. Очевидно, что 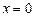 не является корнем уравнения. Разделив числитель и знаменатель каждой дроби на
не является корнем уравнения. Разделив числитель и знаменатель каждой дроби на 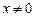 , имеем:
, имеем:
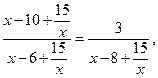 и, сделав замену
и, сделав замену 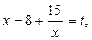 получим:
получим:
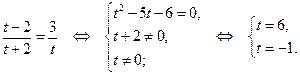
Вернёмся к исходной переменной, имеем:
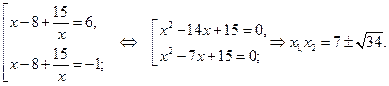
Ответ. 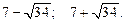
Пример. Решим уравнение: 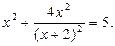
Решение. Выделим полный квадрат суммы:
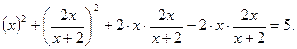
Сгруппируем первый, второй и четвёртый члены:
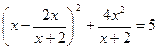 , или
, или 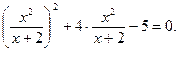
Введем новую переменную. Пусть 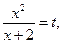 тогда:
тогда: 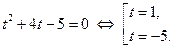
Возвращаясь к исходной переменной, имеем:
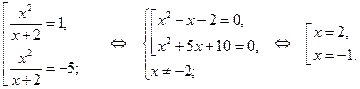
Ответ. 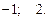
Пример. Решим уравнение: 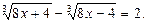
Решение. Введем новые переменные. Пусть 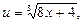
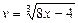 (1)
(1)
Тогда исходное уравнение примет вид: 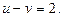
Поскольку введены две новые функции, необходимо найти ещё одно уравнение, связывающее переменные 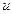 и
и 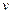 . Для этого возведём оба равенства (1) в куб и заметим, что
. Для этого возведём оба равенства (1) в куб и заметим, что 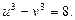 Решим систему:
Решим систему:
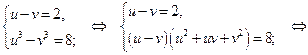
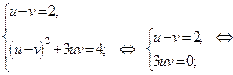
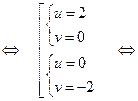
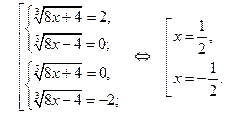
Ответ. 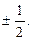
В следующих уравнениях используется “идея однородности”.
Пример. Решим уравнение: 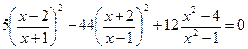 .
.
Решение. Введем новые переменные.
Пусть 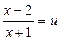 ,
, 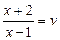 , тогда
, тогда 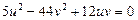 .
.
Если 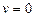 , тогда
, тогда 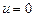 , следовательно,
, следовательно, 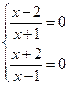
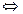
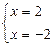 решений нет.
решений нет.
Разделим обе части уравнения на 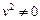 , получим:
, получим: 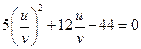 .
.
Решим последнее уравнение, как квадратное относительно 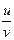 , получим:
, получим:
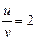 ;
; 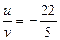 ;
; 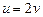 ;
; 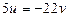 .
.
Возвращаясь к исходным переменным, имеем:
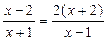 или
или 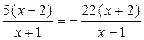
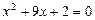
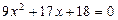
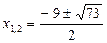 корней нет.
корней нет.
Ответ. 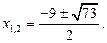
Пример. Решим уравнение: 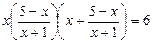
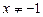
Решение. Введем новые переменные.
Пусть 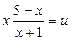 ,
, 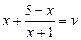 , тогда
, тогда 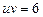 .
.
Найдем 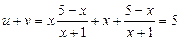 . Составим систему:
. Составим систему: 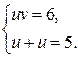
Решая систему подстановкой, получим: 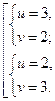
Возвращаясь к исходным переменным, имеем: 
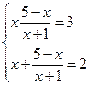
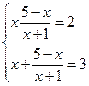
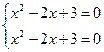
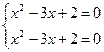
корней нет. 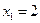 ;
; 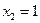
Ответ. 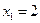 ;
; 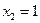
Пример. Решим уравнение: 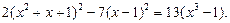
Решение. Очевидно, что 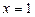 не является корнем уравнения.
не является корнем уравнения.
Разделим обе части уравнения на выражение 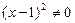 , получим:
, получим:
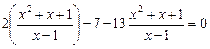 . Введем новую переменную.
. Введем новую переменную.
Пусть 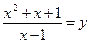 , тогда
, тогда 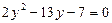 ;
;
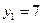 ;
; 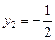 .
.
Возвращаясь к исходной переменной, имеем: 
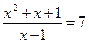 или
или 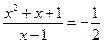
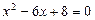
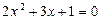
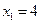 ;
; 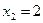
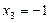 ;
; 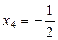
Ответ. 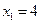 ;
; 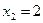 ;
; 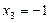 ;
; 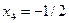
Пример. Решим уравнение: 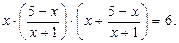
Решение. Введем новые переменные. Пусть 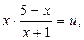
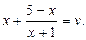 (2)
(2)
Тогда исходное уравнение примет вид 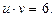
Составим ещё одно уравнение, зависящее от переменных 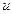 и
и 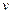 . Для этого найдём сумму:
. Для этого найдём сумму: 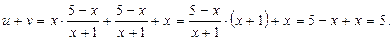
Решим систему: 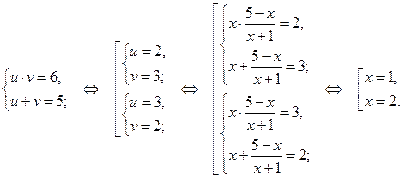
Ответ. 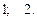
Пример. Решим уравнение: 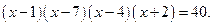
Решение. Заметим, что суммы чисел, стоящих во второй и четвёртой, в первой и третьей скобках, равны, то есть 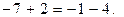 Перемножим эти пары скобок, получим:
Перемножим эти пары скобок, получим: 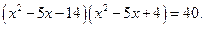
Введем новую переменную. Пусть 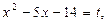 тогда:
тогда: 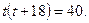
Решим квадратное уравнение 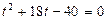 , получим:
, получим: 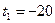 или
или 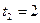 .
.
Вернемся к исходной переменной и решим совокупность уравнений:
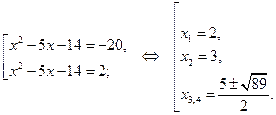
Ответ. 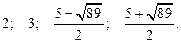
Пример. Решим уравнение: 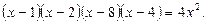
Решение. Заметим, что произведение чисел, стоящих в первой и третьей, во второй и четвёртой скобках, равны, то есть 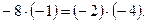
Перемножим указанные пары скобок и запишем уравнение:
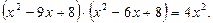
Поскольку 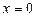 – не является корнем уравнения, разделим обе части уравнения на
– не является корнем уравнения, разделим обе части уравнения на 
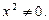 Получим:
Получим: 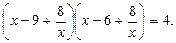
Введем новую переменную.
Пусть 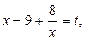 тогда:
тогда: 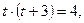 то есть
то есть 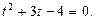
Отсюда 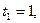
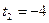 . Возвращаясь к исходной переменной, имеем:
. Возвращаясь к исходной переменной, имеем: 
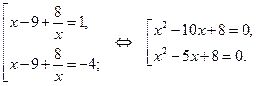
Первое уравнение совокупности имеет корни 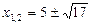 .
.
Второе уравнение не имеет корней.
Ответ. 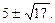
Пример. Решим уравнение: 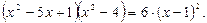
Решение. Данное уравнение можно свести к однородному уравнению. Преобразуем первый множитель, выделив из него выражение, равное второму множителю, то есть 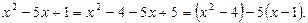
Подставляя последнее выражение в исходное уравнение, получим: 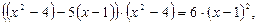 и далее:
и далее: 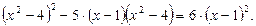
Введем новые переменные. Пусть 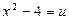 и
и 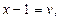 приведём последнее уравнение к виду
приведём последнее уравнение к виду 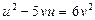 . Это однородное уравнение второй степени относительно
. Это однородное уравнение второй степени относительно 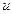 и
и 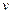 . В нём
. В нём 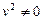 . В самом деле, если
. В самом деле, если 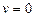 , то уравнение приводится к виду
, то уравнение приводится к виду 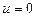 , или
, или 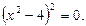
Но система 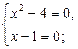 решений не имеет.
решений не имеет.
Разделив обе части уравнения 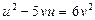 на
на 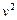
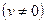 , получим:
, получим:
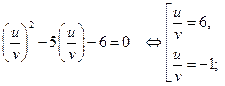
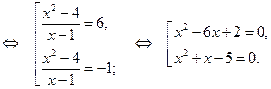
Отсюда 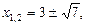
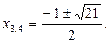
Ответ. 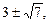
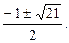
Иногда для решения уравнения вводят тригонометрическую подстановку. Рассмотрим пример.
Пример. Решим уравнение: 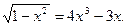
Решение. Функция 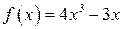 существует при любых значениях
существует при любых значениях 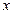 . Найдём область определения функции
. Найдём область определения функции 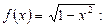
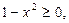 значит,
значит, 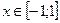 . Введем замену
. Введем замену 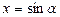 или
или 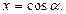
Пусть 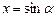 . Необходимо исследовать все значения данной функции. Функция
. Необходимо исследовать все значения данной функции. Функция 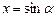 периодическая. Выберем для удобства любой отрезок, на котором функция принимает все свои значения, например отрезок
периодическая. Выберем для удобства любой отрезок, на котором функция принимает все свои значения, например отрезок 
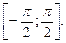
Подставив замену в уравнение, получим:
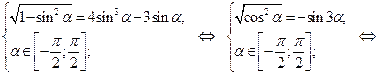
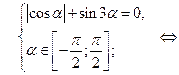
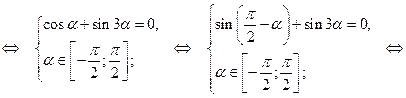
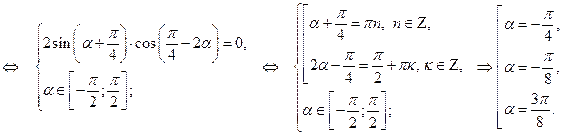
Возвращаясь к исходной переменной, имеем: 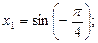
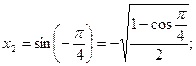
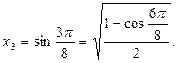
Ответ. 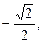
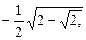
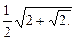
Пример. Решим уравнение: 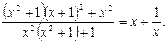
Решение. Выделим наиболее часто повторяющееся выражение 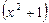 и упростим левую часть исходного уравнения:
и упростим левую часть исходного уравнения: 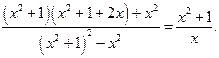
Введём замену: 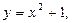 тогда уравнение примет вид:
тогда уравнение примет вид:
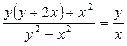 , или
, или 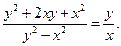
При дальнейших упрощениях получим: 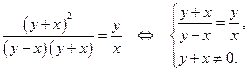
Применим основное свойство дроби к левой части уравнения, разделив на 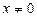 :
: 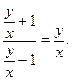 Введём вторую переменную. Пусть
Введём вторую переменную. Пусть 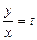 , тогда:
, тогда:
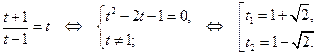
Возвращаясь к исходной переменной, имеем:
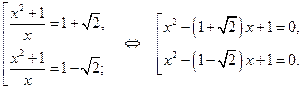
Второе уравнение совокупности не имеет решений, первое имеет два корня 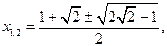 которые и вынесем в ответ.
которые и вынесем в ответ.
Ответ. 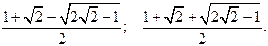
Уравнения вида 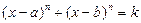 и к ним сводящиеся решаются при помощи замены
и к ним сводящиеся решаются при помощи замены 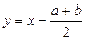
Пример. Решим уравнение: 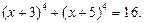
Решение. Введем новую переменную.
Пусть 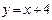 , тогда
, тогда 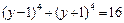 ;
; 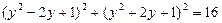 ;
; 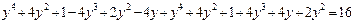 ;
; 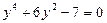 ;
;
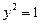 или
или 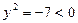 корней нет
корней нет
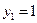 ;
; 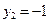
Возвращаясь к исходной переменной, имеем:
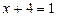 или
или 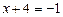
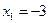
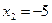
Ответ. 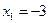 ;
; 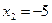
 2015-04-23
2015-04-23 3322
3322
