Умение решать задачи является одним из основных показателей уровня математического развития личности, глубины освоения учебного материала.
При решении ряда задач математические понятия и методы служат аппаратом для решения конкретных проблем. При этом обучаемый, исследуя внематематическую проблему, формулирует различные вопросы и задачи, затем «переводит» их на язык математики (этап построения математической модели), для того чтобы решить их математическими методами (работа внутри математической модели), затем проинтерпретировать решение с учетом проблемы, поставленной в начале (интерпретация дедуктивных рассуждений и расчетов). При этом осуществляется перенос центра тяжести с обучения математике на образование посредством математики.
Задачи − многоаспектное явление обучения, занимающее большое место в учебном процессе и выступающее способом организации управления учебно-познавательной деятельностью обучаемых, носителем действий, адекватных содержанию обучения математике, средством целенаправленного формирования знаний, умений и навыков, одной из форм методов обучения, средством связи теории с практикой.
Задача понимается как объект мыслительной деятельности, содержащий требование практического преобразования или ответа на теоретический вопрос посредством поиска условий, позволяющих на основе построения системы данных, связанных общими законами и категориями, раскрыть отношения между известными и неизвестными ее элементами.
Текстовая задача – есть описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения.
Мы рассматриваем задачу как субъективное, психологическое отражение внешней ситуации, в которой развертывается целенаправленная деятельность субъекта. Процесс решения задач будем рассматривать как сложный аналитико-синтетический процесс направленного взаимодействия субъекта с объективным содержанием решаемой задачи.
Рассматривая задачу в узком смысле этого понятия, в ней можно выделить следующие составные элементы:
– словесное изложение сюжета, в котором явно или в завуалированной форме указана функциональная зависимость между величинами, числовые значения которых входят в задачу;
– числовые значения величин или числовые данные, о которых говорится в тексте задачи;
– задание, обычно сформулированное в виде вопроса, в котором предлагается узнать неизвестные значения одной или нескольких величин. Эти значения называют искомыми.
В процессе решения задач осуществляется теснейшее взаимодействие знаний и действий: знание содержания задачи актуализирует действия по его анализу; действия, преобразуя условие задачи, раскрывая в нем новые стороны, создают предпосылки для отражения этих новых сторон, то есть актуализации новых знаний; те, в свою очередь, актуализируют новые действия и т.д.
Важную роль при решении задач играет моделирование - общенаучный метод познания действительности, при котором для исследования объекта строится его модель, сохраняющая основные, выделенные особенности объекта исследования.
Под математической моделью в общем случае понимают описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Обычно такое математическое описание существенных особенностей изучаемого явления есть уравнение или система уравнений, описывающих элементарные процессы, из которых складывается исследуемое явление. В процессе решения задач человек, как правило, использует определенные совокупности действий. Обычно такую совокупность действий, приводящих к решению задач определенного класса, называют приемом, способом или методом решения. Необходимость формирования у младших школьников умения решать задачи не вызывает сомнений.
В процессе математического моделирования при решении математических задач можно выделить три следующих этапа:
− перевод задачи на язык, подходящей для ее решения математической теории (построение математической модели задачи);
− решение задачи в рамках математической теории, на язык которой она переведена (решение задачи внутри модели);
− обратный перевод результата решения на язык, на котором была сформулирована исходная задача (интерпретация полученного решения).
Деятельность по решению задачи включает следующие этапы независимо от выбранного метода решения.
Выделяют четыре этапа работы над задачами:
− анализ содержания, построение математической модели задачи;
− поиск пути решения задачи и составление плана ее решения;
− осуществление плана решения задачи;
Под планом решения задачи будем понимать описание хода решения данной задачи. Он содержит описание всех необходимых преобразований условий задачи для ее решения, указание всех логических условий применимости каждого из преобразований и указание всех признаков того вида задач, решение которых может быть осуществлено данным методом. Схему или программу, состоящую из системы указаний и ориентиров, пользуясь которыми при встрече с задачей данного вида учащийся может составить план ее решения.
Выделим этапы процесса решения задачи:
- получение информации исходя из содержания данной задачи;
- анализ информации, перевод условий на язык математики;
- выявление проблемной ситуации;
- выявление закономерностей и установление аналогий;
- построение моделей системы;
- поиск процедур решения задачи;
- разработка и прогноз перечня альтернатив и их следствий;
- подбор средств аргументации (например, для обоснования выбора того или иного вероятностного закона);
- корректировка решения;
- реализация решения;
- интерпретация решения с учетом проблемы, поставленной в начале.
Метод или способ решения − это план решения не только данной конкретной задачи, но и всех задач того вида, к которому относится эта задача. Он содержит описание всех необходимых преобразований условий задачи для ее решения, указание всех логических условий применимости каждого из преобразований и указание всех признаков того вида задач, решение которых может быть найдено этим методом. Схему, состоящую из системы указаний, пользуясь которыми при встрече с задачей данного вида учащийся может составить план ее решения или даже алгоритм решения всех задач того типа, к которому относится решаемая задача.
Кратко остановимся на классификации задач. Попытки разбить комплекс учебных задач, решаемых в средней школе, на группы по тому или иному принципу и дать методику решения для каждой группы в отдельности содержатся в работах К.П. Сикорского, И.И. Дырченко, И.Г. Польского, М.Ф. Добрынина и мн.др. В зависимости от целей классификации выбирают основание для ее проведения и на его основе получают те или иные группы математических задач, которые объединяют либо метод решения, либо количество действий, которые необходимо выполнить для решения задачи, либо схожий сюжет и т.п.
В зависимости от выбранного основания задачи можно задачи разделить:
− по числу действий, которые необходимо выполнить для решения задачи;
− по соответствию числа данных и искомых;
− по фабуле задачи;
− по способам решения и др.
Выбрав в качестве основания классификации соответствие числа данных и искомых задачи, выделяют задачи определенные, задачи с альтернативным условием, неопределенные и переопределенные. Чаще всего в задачах число условий (зависимости между величинами) соответствует числу данных и искомых. Но встречаются задачи, в которых этого соответствия нет.
Определенными будем называтьзадачи, в которых условий столько, сколько необходимо и достаточно для получения ответа.
Задачами с альтернативным условием будем называть задачи, в ходе решения которых необходимо рассматривать несколько возможных вариантов условия, а ответ находится после того, как эти возможности будут исследованы.
Задача. Барин говорит своему слуге: «Я задумал три числа, сумма которых равна 100. Сумма двух из них равна 80, а первое число на 20 больше второго. Какие числа я задумал?».
Неопределенными задачами будем называтьзадачи, в которых условий недостаточно для получения ответа.
Задача. Имеется 9 слитков золота и 11 серебра, их взвесили, вес как раз совпадал. Переложили слиток золота и слиток серебра, золото стало легче. Спрашивается, каков вес слитка золота и слитка серебра каждого в отдельности?
В данной задаче недостаточное число данных (в ней нет данных о том, на сколько легче стало золото). Для того чтобы ее решить необходимо дополнительное условие.
Положив в основе классификации фабулу задачи, чаще всего выделяют такие группы задач: «на движение», «на смеси», «на сплавы», «на части», «на время» и т.д. Однако, классифицировать задачи, исходя из фабулы условия, очень сложно, так как тематика условий задач бывает очень разнообразной.
Множество задач, в которых имеется одинаковая зависимость между величинами, входящими в эти задачи, при возможном различии данных и фабул образуют определенный вид задач. Задачи одного вида имеют одну и ту же алгебраическую модель. Положив в основание классификации способы решения задачи, можно выделить такие группы задач как: задачи на «золотое сечение», задачи на пропорциональное деление, задачи на исключение одного из известных, задачи на среднее арифметическое, задачи на проценты и части, задачи, решаемые с конца, или «обратным ходом», и т.д.
Произведем классификацию задач по типу их решения:
− тройное правило (на простое и на сложное тройное правило);
− на нахождение неизвестных по результатам действий (по их сумме и разности, по их сумме и отношению, по разности и их отношению, по двум остаткам или двум разностям, по трем суммам этих неизвестных, взятых попарно);
− на пропорциональное деление;
− на исключение одного из неизвестных;
− на среднеарифметическое;
− на проценты;
− задачи, решаемые с конца, или обратным ходом;
− задачи на работу;
− задачи на смеси;
− на вычисление времени;
− геометрического содержания.
При решении задач различными методами используют, как правило, «свою» классификацию задач. Так, при алгебраическом методе решения чаще всего в качестве основания классификации рассматривают фабулу задачи, а при решении арифметическим методом задач делят их по способам решения. Однако следует отметить, что такое разбиение задач на группы, строго говоря, не является классификацией, так как в этих случаях, с одной стороны, появляются задачи, которые не могут быть отнесены ни к одной из образовавшихся групп, с другой стороны, существуют задачи, которые могут быть отнесены к нескольким указанным группам. Вместе с тем с точки зрения учебных целей эти и подобные классификации задач удобны. Они дают возможность выделить наиболее типичные виды задач и усвоить стандартные способы их решения.
Говоря о методах решения задачи, мы имеем в виду два их вида: методы, присущие науке математике, исходящие из ее содержания (например, алгебраический, арифметический, геометрический и т.д.), и методы научного познания (анализ, синтез, аналогия, обобщение и т.д.). Под алгебраическим методом решения задач понимают метод решения, при котором неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или системы неравенств, составленных по условию задачи.
Алгебраический метод решения текстовых задач позволяет развивать умение анализировать задачные ситуации, строить план решения с учетом взаимосвязей между известными и неизвестными величинами (с учетом типа задачи), истолковывать результат каждого действия в рамках условия задачи, проверять правильность решения с помощью составления и решения обратной задачи, то есть, формировать и развивать важные общеучебные умения. При решении задач алгебраическим методом основную мыслительную деятельность сосредотачивают на первом этапе решения задачи: на разборе условия задачи и составлении уравнений или неравенств по условию задачи.
На этапе анализа условия задачи:
– разбивают условие задачи на части;
– выясняют, какие величины характеризуют описываемый процесс;
– выясняют, какие величины известны, а какие требуется найти;
– устанавливают связи между величинами.
На этапе поиска решения выясняют, что можно найти по данным задачи, и поможет ли это дальнейшему решению.
Завершают этап поиска составлением плана решения задачи.
Вторым этапом является решение составленного уравнения или системы уравнений, неравенства или системы неравенств.
Третьим важным этапом решения задач является проверка решения задачи, которая проводится по условию задачи.
Обратим внимание на то, что при перечислении этапов, которые проходят при поиске решения задачи алгебраическим методом, сначала был назван выбор условия для составления уравнения, затем составление схемы уравнения, и только тогда мы вводим переменную. На практике происходит иначе: сначала вводят переменную, затем выражают остальные величины через нее и затем составляют уравнение.
Задача. Из села в город, расстояние между которыми 116 лье, отправляются курьеры с заданиями. Скорость первого курьера 12 лье в час, второго, имеющего срочное задание − 32 лье в час. Определим, через какое время первому курьеру останется проехать путь в 4 раза больший, чем второму, со срочным заданием?
Анализ задачи. В задаче идет речь о двух курьерах, которые отправляются одновременно в одном направлении из села в город. Известно, что расстояние между селом и городом равно 116 лье, скорость первого курьера − 12 лье в час, скорость второго − 32 лье в час. Требуется узнать, через какое время первому курьеру останется проехать путь в 4 раза больший, чем второму.
Краткая запись задачи (схематический чертеж) показана на рисунке.
Поиск пути решения задачи и составление плана ее решения. Обозначим искомое время через х часов. Зная скорость второго курьера, можем узнать, какое расстояние он проедет за х часов. Зная, расстояние между селом и городом, найдем, какое расстояние останется проехать второму до города.
По условию первому курьеру останется проделать путь, в четыре раза больший, чем второму. Следовательно, можем составить уравнение, приравняв между собой путь, который осталось проехать первому курьеру, и путь, в четыре раза больший пути, который осталось проехать второму.
Решив уравнение, найдем, через какое время первому курьеру останется пройти путь в четыре раза больший, чем второму курьеру.
Осуществление плана решения задачи. Пусть через 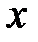 часов первому останется проделать путь в четыре раза больший путь, чем второму. За это время второй курьер проедет
часов первому останется проделать путь в четыре раза больший путь, чем второму. За это время второй курьер проедет 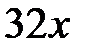 лье, значит, ему останется проехать до города
лье, значит, ему останется проехать до города 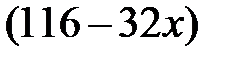 лье. Первый за
лье. Первый за 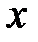 часов проедет
часов проедет 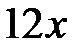 лье, значит, ему останется проехать до города
лье, значит, ему останется проехать до города 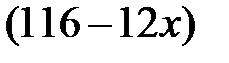 лье.
лье.
По условию это расстояние в четыре раза больше, чем расстояние, которое останется проехать второму курьеру.
Следовательно, получим уравнение: 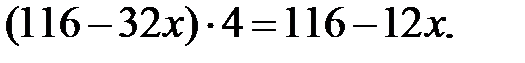
После несложных преобразований, имеем: 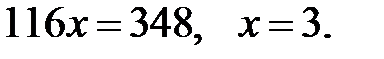
Итак, искомое время равно 3 часа.
Проверка решения задачи. Через 3 часа второй курьер пройдет 32? 3 = 96(лье), останется 116 − 96 = 20(лье). Через 3 часа первый курьер пройдет 12? 3 = 36(лье), останется до конца 116 − 36 = 80(лье). Найдем, во сколько раз первому курьеру останется сделать больший путь, чем второму: 80: 20 = 4 (раза). Расхождения с условием задачи нет, следовательно, задача решена правильно.
Ответ. 3 часа.
В реальном процессе решения задачи, названные этапы не имеют четких границ, их не всегда выделяют в явном виде, переходя от одного к другому незаметно. Вместе с тем решение каждой отдельно взятой задачи, как правило, содержит все указанные этапы, осмысленное прохождение которых, вместе со знанием приемов их выполнения, делает процесс решения любой задачи осознанным и целенаправленным. Игнорирование одних этапов (например, поиска пути решения) может привести к решению методом «проб и ошибок», игнорирование других (например, проверки решения задачи) − к получению неверного ответа и т.д.
Рассмотрим примеры решения задач алгебраическим методом.
Задача. Поезд был задержан у семафора на 16 минут. Чтобы прийти в пункт назначения вовремя, поезд компенсировал опоздание на перегоне 192 км, идя со скоростью, превышающей на 10 км/ч положенную по расписанию. Найдем скорость поезда по расписанию.
Решение. Пусть 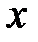 км/ч – скорость поезда по расписанию, тогда 192 км поезд должен пройти за
км/ч – скорость поезда по расписанию, тогда 192 км поезд должен пройти за 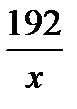 ч, однако он прошел это расстояние за
ч, однако он прошел это расстояние за 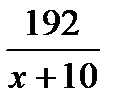 ч, компенсировав задержку в 16 мин. 16 мин =
ч, компенсировав задержку в 16 мин. 16 мин = 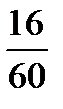 (ч)=
(ч)= 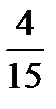 (ч).
(ч).
Это позволяет составить уравнение: 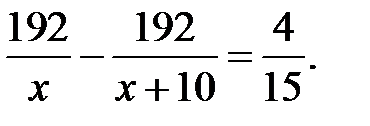 Решим данное уравнение:
Решим данное уравнение: 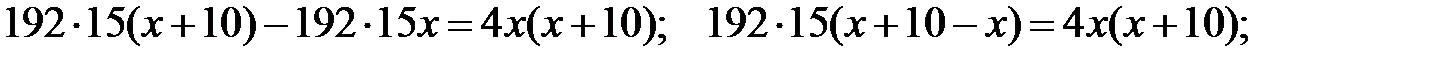
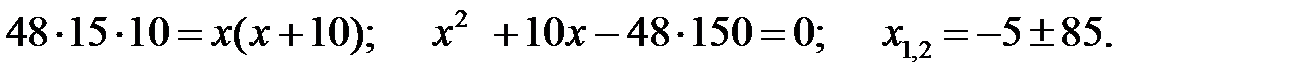
Так как по условию 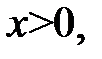 то
то 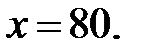
Проверка показывает, что скорость поезда по расписанию 80 км/ч
Ответ. 80 км/ч
Задача. Рабочий день на фабрике уменьшили с 8 до 7 часов, при этом количество выпускаемой продукции за день увеличили на 5%. Найдем, на сколько процентов увеличилась производительность труда.
Решение. Пусть 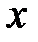 – первоначальная производительность труда, а
– первоначальная производительность труда, а 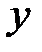 – производительность труда после сокращения рабочего дня. По условию задачи не требуется находить производительности, а только их отношение, поэтому составим уравнение с двумя неизвестными:
– производительность труда после сокращения рабочего дня. По условию задачи не требуется находить производительности, а только их отношение, поэтому составим уравнение с двумя неизвестными: 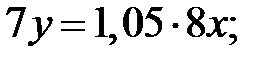
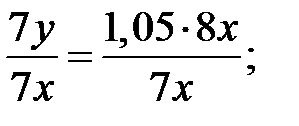
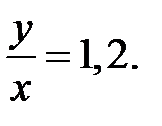
Следовательно, производительность труда выросла на 20%.
Ответ. 20%.
Задача. Морская вода содержит 5% соли. Определим сколько килограммов пресной воды необходимо добавить к 20 кг морской воды, чтобы концентрация соли в смеси составила 2%?
Решение. В 20 кг морской воды содержится соли 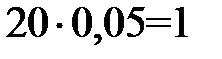 (кг). Пусть нужно добавить
(кг). Пусть нужно добавить 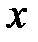 кг пресной воды, тогда смеси будет
кг пресной воды, тогда смеси будет 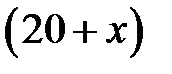 кг, содержание соли 1 кг. Зная, что это составляет 2%, составим уравнение:
кг, содержание соли 1 кг. Зная, что это составляет 2%, составим уравнение:
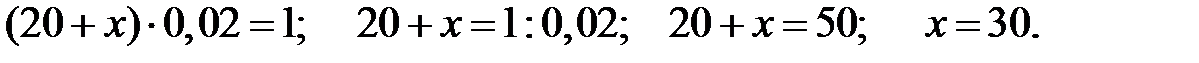
Необходимо добавить 30 кг пресной воды.
Ответ. 30 кг.
Задача. Двузначное число разделили на сумму его цифр, в частном получили 3, а в остатке 5. Найдем это число.
Решение. 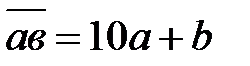 – число,
– число, 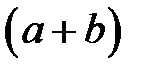 – сумма цифр этого числа.
– сумма цифр этого числа.
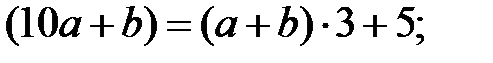 делитель
делитель 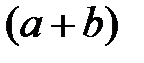 больше остатка 5 и так как самая большая цифра 9, то
больше остатка 5 и так как самая большая цифра 9, то 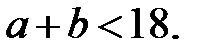
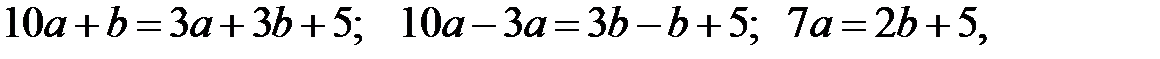 значит,
значит, 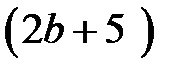 делится на 7, так как
делится на 7, так как 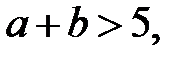 то
то 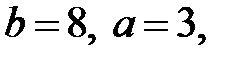 то есть
то есть 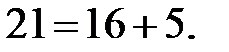
Искомое двузначное число 38.
Ответ. 38
Задача. Длину прямоугольника уменьшили на 20%. Определим, на сколько процентов необходимо увеличить ширину, чтобы площадь не уменьшилась.
Решение. Пусть 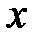 – длина прямоугольника,
– длина прямоугольника, 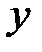 – ширина, тогда
– ширина, тогда 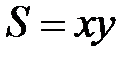 – площадь прямоугольника.
– площадь прямоугольника.
Измененная длина: 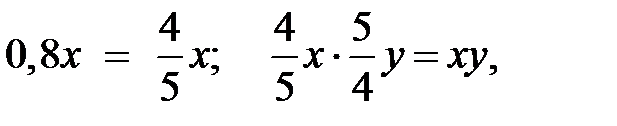 измененная ширина –
измененная ширина – 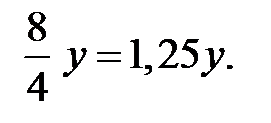 Таким образом, ширину необходимо увеличить на 25%.
Таким образом, ширину необходимо увеличить на 25%.
Ответ. 25%.
Заметим, что многие задачи, которые можно решить, составляя уравнение с одним неизвестным, можно проще с помощью систем уравнений.
Задача. Путь от пункта А до пункта В автомобиль проезжает на 3 ч 12 мин быстрее мотоцикла. За то время, когда мотоцикл проезжает путь от А до В, автомобиль проходит на 288 км больше мотоцикла. Если скорость каждого увеличить на 10 км/ч, то автомобиль пройдет от А до В на 2 ч 24 мин быстрее мотоцикла. Определим расстояние от пункта А до пункта В.
Решение. Обозначим скорость автомобиля за 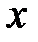 км в час, скорость мотоцикла – за
км в час, скорость мотоцикла – за 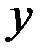 км в час, расстояние от пункта А до пункта В –
км в час, расстояние от пункта А до пункта В – 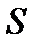 км. Тогда время прохождения расстояния от А до В для автомобиля равно
км. Тогда время прохождения расстояния от А до В для автомобиля равно 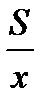 ч, время прохождения расстояния от А до В для мотоцикла равно
ч, время прохождения расстояния от А до В для мотоцикла равно 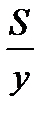 ч.
ч.
Зная, что время затраченное автомобилем меньше времени затраченного мотоциклом на 3 ч 12 мин или на 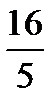 ч, составим уравнение:
ч, составим уравнение: 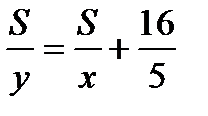 .
.
Мотоцикл проезжает путь за 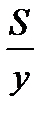 ч, автомобиль за это время проходит
ч, автомобиль за это время проходит 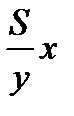 км, что на 288 км больше, чем
км, что на 288 км больше, чем 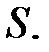 Составим второе уравнение:
Составим второе уравнение: 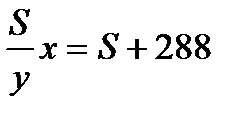 .
.
После увеличения скорости автомобиля и мотоцикла станут 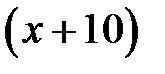 км/ч и
км/ч и 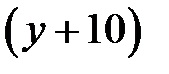 км/ч соответственно, время затраченное автомобилем:
км/ч соответственно, время затраченное автомобилем: 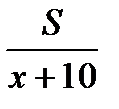 ч., время затраченное мотоциклом
ч., время затраченное мотоциклом 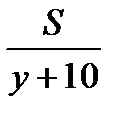 ч.
ч.
Зная, что время затраченное автомобилем на 2 часа 24 минуты= 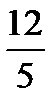 часа меньше, составим третье уравнение:
часа меньше, составим третье уравнение: 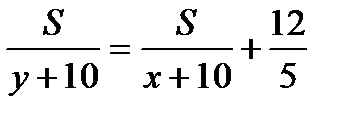 .
.
Так как переменные 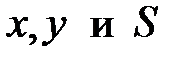 , в составленных уравнениях, означают одни и те же величины, получим систему трех уравнений с тремя неизвестными:
, в составленных уравнениях, означают одни и те же величины, получим систему трех уравнений с тремя неизвестными:
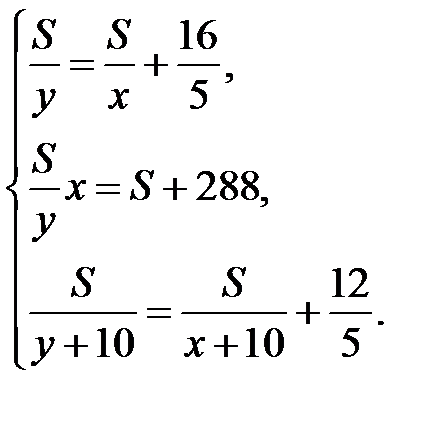 .
.
Выразим 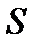 из первого и второго уравнений и приравняем полученные выражения:
из первого и второго уравнений и приравняем полученные выражения: 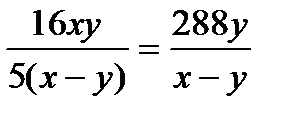 . Из уравнения найдем скорость автомобиля:
. Из уравнения найдем скорость автомобиля: 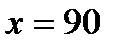 (км/ч).
(км/ч).
Выразим 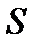 из первого и третьего уравнений и приравняем полученные выражения:
из первого и третьего уравнений и приравняем полученные выражения: 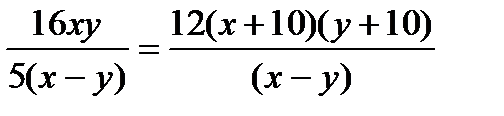 .
.
Подставив в уравнение найденное значение скорости автомобиля, найдем скорость мотоцикла: 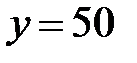 , 50 км/ч.
, 50 км/ч.
Подставив найденные значения 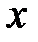 и
и 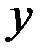 , находим расстояние от пункта А до пункта В:
, находим расстояние от пункта А до пункта В: 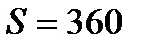 .
.
Ответ. 360 км.
К задачам «на работу» относят задачи, где речь о выполнении какой-либо работы: заполнении бассейна, выкапывании котлована, перепечатывании рукописи и т.д. Задачи на «работу» делят на два вида: задачи, в которых ничего не известно об объеме работы, и задачи, в которых объем работы указан.
Если об объеме работы ничего неизвестно, то всю работу принимают за 1 условную единицу, за переменные выбирают производительность за единицу времени.
Задача. Двое рабочих выполнили работу за два дня. Если бы первый рабочий проработал 2 дня, а второй 1 день, то они вместе выполнили бы 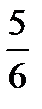 всей работы. Определим, за сколько дней выполнит эту работу первый рабочий?
всей работы. Определим, за сколько дней выполнит эту работу первый рабочий?
Решение. Обозначим всю работу за 1 условную единицу, производительность за 1 день первого рабочего за 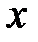 , производительность второго рабочего за 1 день за
, производительность второго рабочего за 1 день за 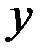 .
.
Тогда, работая вдвоем, рабочие за 1 день выполнят 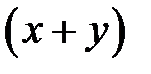 всей работы. На выполнение всей работы им потребуется
всей работы. На выполнение всей работы им потребуется 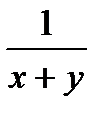 дней. Зная, что рабочие выполнили работу за два дня, составим уравнение:
дней. Зная, что рабочие выполнили работу за два дня, составим уравнение: 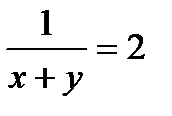 .
.
За два дня первый рабочий выполнит 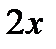 всей работы, за один день второй рабочий выполнит
всей работы, за один день второй рабочий выполнит 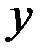 всей работы. Зная, что если бы первый рабочий проработал 2 дня, а второй – 1 день, то они вместе выполнили бы
всей работы. Зная, что если бы первый рабочий проработал 2 дня, а второй – 1 день, то они вместе выполнили бы 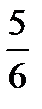 всей работы, составим уравнение:
всей работы, составим уравнение: 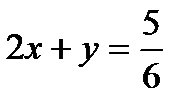 .
.
Так как переменные 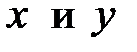 , в составленных уравнениях, означают одни и те же величины, получим систему уравнений:
, в составленных уравнениях, означают одни и те же величины, получим систему уравнений: 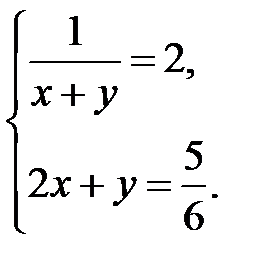 .
.
Решая систему, найдем производительности рабочих: 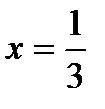 ,
, 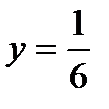 .
.
Тогда время, которое затратит первый рабочий на выполнение всей работы равно: 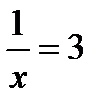 , за 3 дня выполнит работу первый рабочий.
, за 3 дня выполнит работу первый рабочий.
Ответ. За 3 дня.
Задача. Ученик прочел книгу в 480 страниц, ежедневно читая одинаковое количество страниц. Если бы он читал каждый день на 16 страниц больше, то прочел бы книгу на 5 дней раньше. Сколько дней ученик читал книгу?
Решение. Пусть ученик читал в день 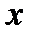 страниц. Тогда он прочитал всю книгу за
страниц. Тогда он прочитал всю книгу за 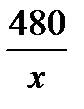 дней. Если бы он читал
дней. Если бы он читал 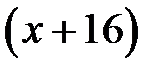 страниц в день, то он прочитал бы книгу за
страниц в день, то он прочитал бы книгу за 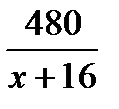 дней, что на 5 дней меньше. Составим уравнение:
дней, что на 5 дней меньше. Составим уравнение: 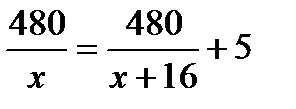 .
.
Решим его, получим 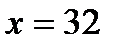 , то есть ученик в день читал 32 страницы и прочитал книгу за 15 дней.
, то есть ученик в день читал 32 страницы и прочитал книгу за 15 дней.
Ответ. 15 дней.
Задача. Двое рабочих выполнили работу менее, чем за 4 часа. Если бы первый выполнял ее в одночку, он сделал бы работу на 6 часов быстрее, чем второй. Какие значения может принимать время выполнения работы первым из рабочих, работающим отдельно?
Решение. Обозначим всю работу за 1 условную единицу, производительность за день первого рабочего за 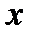 , а производительность второго рабочего за день за
, а производительность второго рабочего за день за 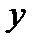 . Тогда, работая вдвоем, рабочие за день сделают
. Тогда, работая вдвоем, рабочие за день сделают 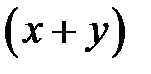 . На выполнение всей работы им потребуется
. На выполнение всей работы им потребуется 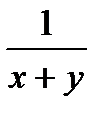 дней. Зная, что двое рабочих выполнили работу менее, чем за 4 часа, составим неравенство:
дней. Зная, что двое рабочих выполнили работу менее, чем за 4 часа, составим неравенство: 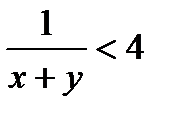 .
.
Время, за которое может выполнить работу первый рабочий выражается: 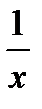 , а время второго:
, а время второго: 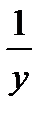 . Зная, что если бы первый работал в одночку, он сделал бы работу на 6 часов быстрее, чем второй, составим уравнение:
. Зная, что если бы первый работал в одночку, он сделал бы работу на 6 часов быстрее, чем второй, составим уравнение: 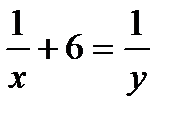 .
.
Так как переменные 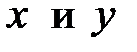 , в составленных уравнениях, означают одни и те же величины, получим систему уравнений:
, в составленных уравнениях, означают одни и те же величины, получим систему уравнений: 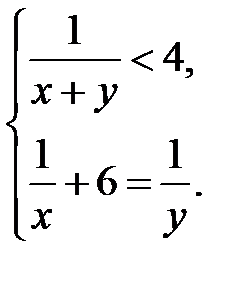 .
.
Так как производительность – величина положительная, то неравенства в системе равносильно следующему: 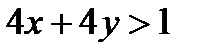 .
.
Выразим 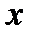 из уравнения и подставим в неравенство:
из уравнения и подставим в неравенство: 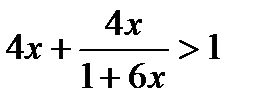 . Решая это неравенство, получаем:
. Решая это неравенство, получаем: 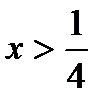 или
или 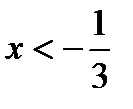 . Условию соответствует первое неравенство. Следовательно,
. Условию соответствует первое неравенство. Следовательно, 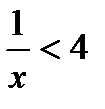 .
.
Ответ. Время выполнения работы первым из рабочих, работающим отдельно, может принимать значения, не большие 4.
При решении задач на проценты и отношения необходимо помнить, что можно приравнивать количественные величины: килограммы, метры и т.д., но не проценты. При решении таких задач полезно составлять таблицу.
Задача. В свежей ягоде содержится 90% воды, в сушеной – 10% воды. Найдем, сколько сушеной ягоды можно получить из 18 кг свежей.
Решение. Ягода состоит из сухого вещества и воды. Составим таблицу.
| Сухое вещество | Вода | Общая масса | |
| Свежая ягода | 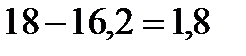 | 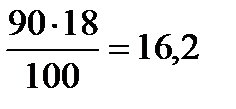 | 18кг |
| Сушеная ягода | 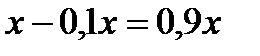 | 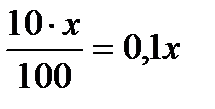 | 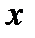 кг кг |
Неизменным в процессе сушки остается количество сухого вещества, получим уравнение: 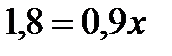 , следовательно,
, следовательно, 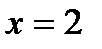 ; 2кг сушеной ягоды можно получить из 18 кг свежей.
; 2кг сушеной ягоды можно получить из 18 кг свежей.
Ответ. 2 кг.
Задача. Сколько литров воды необходимо добавить к 20 кг 5%-ного раствора соли, чтобы получить 4%-ный раствор?
Решение. Раствор состоит из соли и воды. Составим таблицу.
| 5%-ный раствор | Вода | 4%-ный раствор | |
| Общее количество | 20 кг | 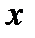 кг кг | 20+ 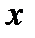 кг кг |
| Соль | 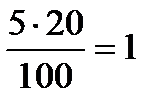 кг кг | 0 | 1 кг |
Соль массой 1 кг составляет 4% от массы 4%-ного раствора, получаем уравнение: 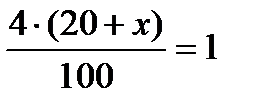 ,
, 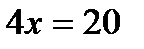 ,
, 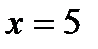 ; 5 литров воды надо добавить к 20 кг 5%-ного раствора соли, чтобы получить 4%-ный раствор.
; 5 литров воды надо добавить к 20 кг 5%-ного раствора соли, чтобы получить 4%-ный раствор.
Ответ. 5 литров.
Задача. Смешали 30%-ный раствор соляной кислоты с 10%-ным и получили 1200 г 15%-ного раствора. Сколько граммов каждого раствора было взято?
Решение. Раствор состоит из кислоты и воды. Составим таблицу.
| 30%-ный раствор | 10%-ный раствор | 15%-ный раствор | |
| Общее количество | 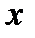 г г | 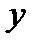 г г | 1200 г |
| Кислота | 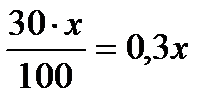 г г | 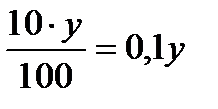 г г | 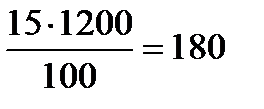 г г |
| Вода | 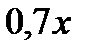 г г | 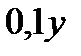 г г | 1020 г |
Получим систему уравнений: 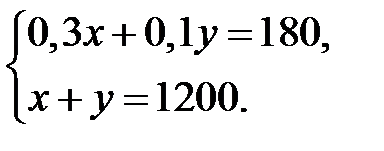 .
.
Решая систему, имеем: 30%-ного раствора взято 300 г, 10%-ного раствора – 900 г.
Ответ. 30%-ного раствора взято 300 г, 10%-ного раствора – 900 г.
Задача. Из двух кусков сплавов золота и серебра с соотношением масс этих металлов 1:2 и 2:3 получили новый сплав массой 95 г с соотношением масс золота и серебра 7:12. Сколько граммов каждого сплава было взято?
Решение. Составим таблицу.
| I сплав | II сплав | III сплав | |
| Общая масса | 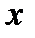 г г | 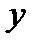 г г | 95 г |
| Золото | 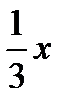 г г | 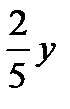 г г | 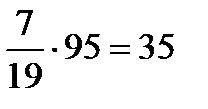 г г |
| Серебро | 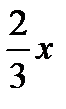 г г | 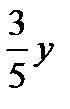 г г | 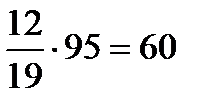 г г |
Получим систему уравнений: 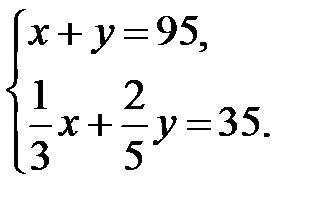 .
.
Решая систему, находим: первого сплава взято 40 г, второго – 50 г.
Ответ. Первого сплава было взято 40 г, второго – 50 г.
Рассмотрим алгебраический метод решения задач, в процессе работы над которыми используются неравенства. Большинство таких задач решаются «в целых числах» или в ответе требуется указать диапазон возможных значений, если по условию задачи допустимо дробное значение переменной. В задачах «в целых числах» говорится о неделимых величинах: например, «в двух бригадах не более 28 человек…»
Задача. Аэролинию, связывающую города А и В, обслуживают самолеты трех типов. Каждый самолет первого, второго и третьего типа может взять на борт 230, 110, 40 пассажиров и 27, 12, 5 контейнеров соответственно. Все самолеты линии могут принять на борт одновременно 760 пассажиров и 88 контейнеров. Найдем число самолетов на линии, если известно, что количество самолетов каждого типа не меньше 2.
Решение. Пусть на линии задействовано 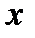 самолетов первого типа,
самолетов первого типа, 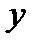 самолетов вторго типа и
самолетов вторго типа и 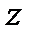 самолетов третьего типа. По условию задачи составим систему:
самолетов третьего типа. По условию задачи составим систему: 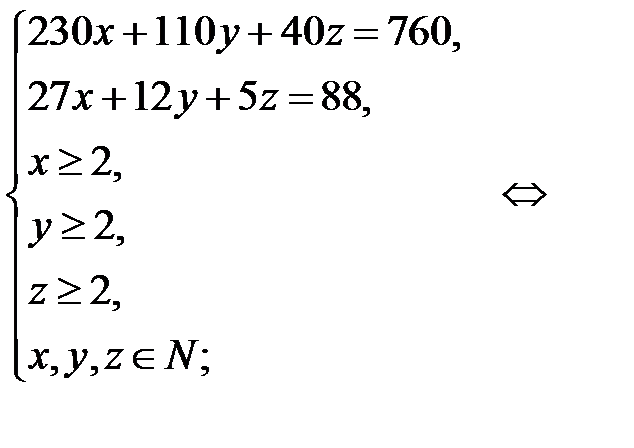
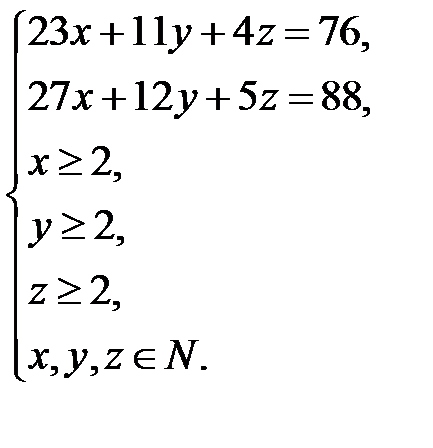 .
.
Рассмотрим второе уравнение 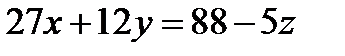 . Левая часть уравнения кратна 3, значит, выражение
. Левая часть уравнения кратна 3, значит, выражение 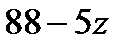 должно делиться на 3. Из этого условия получаем возможные значения для
должно делиться на 3. Из этого условия получаем возможные значения для 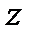 : 2, 5, 8, 11, 14, 17. Для последних трех значений (11, 14, 17) значение выражения
: 2, 5, 8, 11, 14, 17. Для последних трех значений (11, 14, 17) значение выражения 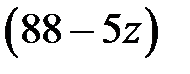 меньше 39 (27+12). Значит, переменная
меньше 39 (27+12). Значит, переменная 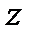 не может принимать эти значения, в противном случае значение одной из переменных
не может принимать эти значения, в противном случае значение одной из переменных 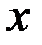 или
или 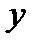 должно быть равно нулю, а это противоречит условию о наличии самолетов трех типов. Итак,
должно быть равно нулю, а это противоречит условию о наличии самолетов трех типов. Итак, 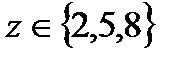 Для каждого из этих значений переменной
Для каждого из этих значений переменной 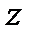 решим систему и найдем значения переменных
решим систему и найдем значения переменных 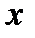 и
и 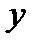 , составим таблицу:
, составим таблицу:
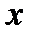 | 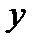 | 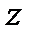 |
| 2 | 2 | 2 |
| 1 | 3 | 5 |
| 0 | 4 | 8 |
Из таблицы видим, что условию задачи удовлетворяют значения: 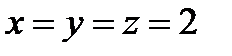 . Итак, на линии 6 самолетов.
. Итак, на линии 6 самолетов.
Ответ. 6 самолетов.
Задача. Трое мальчиков хотели вместе купить две одинаковые игрушки. Сложив все имеющиеся у них деньги, мальчики не могли купить даже одну игрушку. Если бы у первого мальчика было вдвое больше денег, то им на покупку не хватило бы 34 рублей. Когда третьему мальчику добавили денег в размере в два раза большем, чем у него было, то после покупки игрушек у детей оставалось 6 рублей. Сколько стоили игрушки, если первоначально у второго мальчика было на 9 рублей больше, чем у первого?
Решение. Пусть 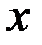 руб. – количество денег у первого мальчика,
руб. – количество денег у первого мальчика, 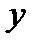 руб. – у второго,
руб. – у второго, 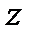 руб. – у третьего,
руб. – у третьего, 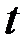 руб. – цена одной игрушки. По условию задачи составим систему уравнений и неравенств:
руб. – цена одной игрушки. По условию задачи составим систему уравнений и неравенств: 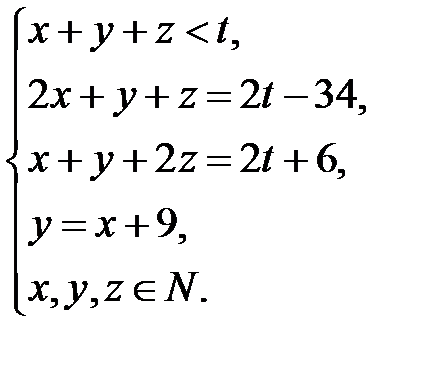
Подставив выражение 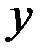 пункта через
пункта через 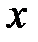 в уравнения, получаем систему:
в уравнения, получаем систему: 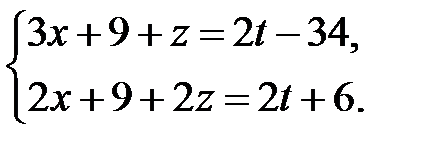 Вычитая из второго уравнения первое и преобразовывая полученной уравнение, находим выражение для
Вычитая из второго уравнения первое и преобразовывая полученной уравнение, находим выражение для 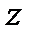 через
через 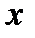 :
: 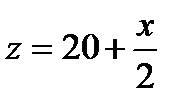 , так как
, так как 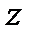 – величина целая, то и
– величина целая, то и 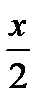 должно быть целым числом, значит,
должно быть целым числом, значит, 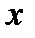 – четное. Подставляя выражение для
– четное. Подставляя выражение для 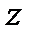 в любое из двух уравнений второй системы, получим выражение для
в любое из двух уравнений второй системы, получим выражение для 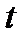 :
: 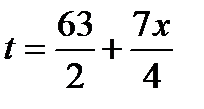 .
.
Подставим выражения для 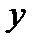 ,
, 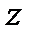 и
и 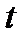 в неравенство и решим полученное неравенство.
в неравенство и решим полученное неравенство. 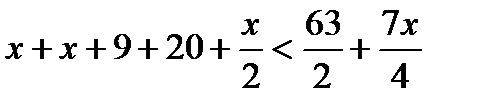 или
или 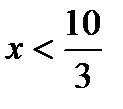 . Значит, переменная
. Значит, переменная 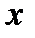 может принимать значения 1, 2 или 3. Условию четности соответствует только значение
может принимать значения 1, 2 или 3. Условию четности соответствует только значение 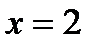 . Подставляя это значение в выражение для
. Подставляя это значение в выражение для 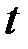 , находим
, находим 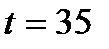 .
.
Итак игрушки стоили по 35 рублей, покупка стоила 70 рублей.
Ответ. 70 рублей.
Задача. Бригаде водителей грузовиков необходимо перевезти груз от 170 до 195 т. Однако, два грузовика в пути сломались, поэтому, чтобы доставить весь груз, пришлось в остальные грузовики догрузить по одной тонне. Сколько груза было перевезено, если все грузовики были одинаково загружены?
Решение. Пусть 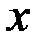 т – количество груза,
т – количество груза, 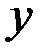 – количество грузовиков. По условию задачи:
– количество грузовиков. По условию задачи: 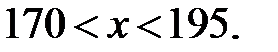
До поломки на каждый грузовик было загружено по 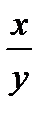 т груза, после поломки –
т груза, после поломки – 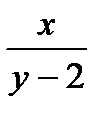 т. Зная, что из-за поломки одного грузовикапришлось догрузить в остальные грузовики по одной тонне груза, составим уравнение:
т. Зная, что из-за поломки одного грузовикапришлось догрузить в остальные грузовики по одной тонне груза, составим уравнение: 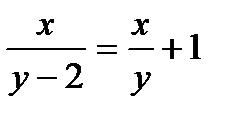 .
.
Так как переменные 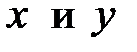 , в составленных уравнении и неравенстве, означают одни и те же величины, получим систему:
, в составленных уравнении и неравенстве, означают одни и те же величины, получим систему: 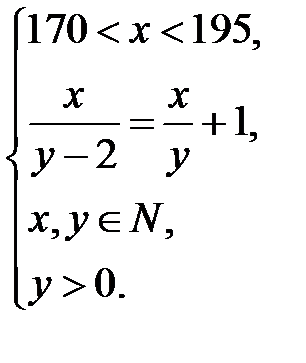
Из уравнения выразим переменную 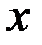 через
через 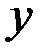 , имеем:
, имеем: 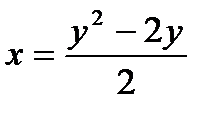 , подставим полученное выражение в неравенство:
, подставим полученное выражение в неравенство: 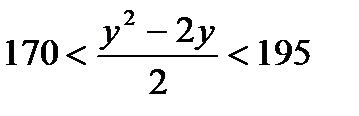 или
или 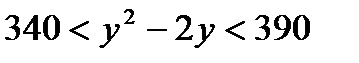 .
.
Полученное двойное неравенство равносильно системе неравенств: 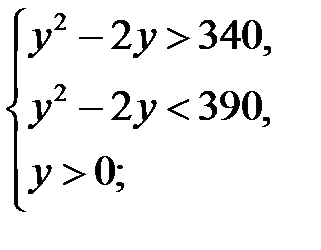 решая эту систему, находим:
решая эту систему, находим: 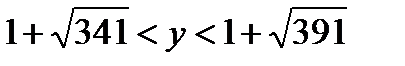 . Несложно убедиться, что в промежутке
. Несложно убедиться, что в промежутке 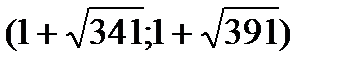 находится единственное целое число
находится единственное целое число 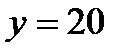 . Итак, в бригаде бывло 20 грузовиков. Подставляя найденное значение
. Итак, в бригаде бывло 20 грузовиков. Подставляя найденное значение 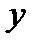 в выражение для
в выражение для 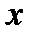 , получаем ответ: 180 т.
, получаем ответ: 180 т.
Ответ. 180 т.
Задача. Автомобиль, едущий с постоянной скоростью из пункта А в пункт 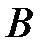 , был задержался в пробке на 24 мин на расстоянии 96 км от
, был задержался в пробке на 24 мин на расстоянии 96 км от 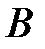 . При каких значениях первоначальной скорости автомобиль приедет в
. При каких значениях первоначальной скорости автомобиль приедет в 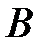 не позже запланированного срока, если после задержки он увеличил скорость на 12 км/ч?
не позже запланированного срока, если после задержки он увеличил скорость на 12 км/ч?
Решение. 24 мин=0,4ч. Пусть 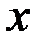 – начальная скорость автомобиля,
– начальная скорость автомобиля, 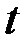 – запланированное время прибытия в пункт
– запланированное время прибытия в пункт 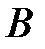 . Если бы автомобиль не уваличил скорость после задержки, то он прибыл бы в
. Если бы автомобиль не уваличил скорость после задержки, то он прибыл бы в 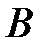 на 0,4 часа позже. Получим уравнение:
на 0,4 часа позже. Получим уравнение: 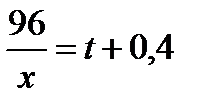 .
.
По условию задачи, автомобиль увеличил скорость, следовательно он преодолел 96 км за 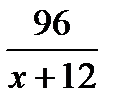 ч. Требуется найти значения переменной
ч. Требуется найти значения переменной 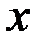 , прикоторых выполнено условие:
, прикоторых выполнено условие: 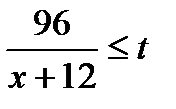 . Получим систему:
. Получим систему: 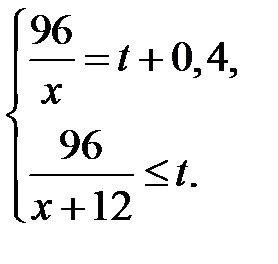
Из условия задачи следует, что 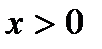 .
.
Из уравнения выразим 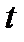 и подставим в неравенство:
и подставим в неравенство: 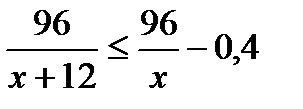 . Решая неравенство, находим:
. Решая неравенство, находим: 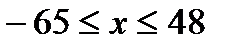 .
.
Учитывая условие 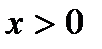 , получим ответ:
, получим ответ: 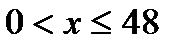 .
.
Ответ. 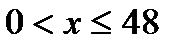 .
.
К смешанномутипу относят задачи, которые по условию должны принадлежать одному типу (например, «на движение»), а по решению – другому (например, к задачам на «работу»).
Задача. Средняя скорость победителя автомобильных гонок оказалась на 20 км/ч выше средней скорости автомобиля, занявшего последнее место. Если бы последний участник преодолевал каждый километр на 1 секунду быстрее, то сократил бы разрыв во времени от победителя в два раза. Найдем скорость победителя.
Решение. Обозначим за 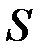 км длину трассы, за
км длину трассы, за 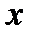 км/ч – скорость проигравшего, тогда скорость победителя равна
км/ч – скорость проигравшего, тогда скорость победителя равна 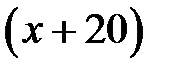 км/ч.
км/ч.
Время победителя – 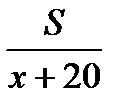 ч, время проигравшего –
ч, время проигравшего – 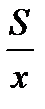 ч.
ч.
Если бы проигравший преодолевал каждый километр на 1 секунду= 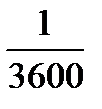 часа быстрее, то на прохождение трассы ему бы потребовалось
часа быстрее, то на прохождение трассы ему бы потребовалось 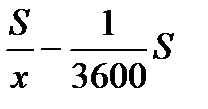
Зная, что если бы последний участник преодолевал каждый километр на 1 секунду быстрее, то сократил бы разрыв во времени от победителя в два раза, составим уравнение: 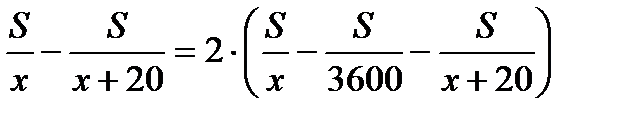 . Корнями уравнения являются:
. Корнями уравнения являются: 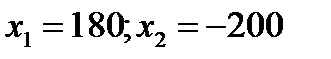 . Второй корень не удовлетворяет условию задачи. Итак, скорость проигравшего 180 км/ч, скорость победителя – 200 км/ч.
. Второй корень не удовлетворяет условию задачи. Итак, скорость проигравшего 180 км/ч, скорость победителя – 200 км/ч.
Ответ. 200 км/ч.
 2015-04-23
2015-04-23 11321
11321
