Тема 1: «Вероятность случайного события»

Всевозможные исходы опыта ω_i (i = 1, 2,…,n ) называются элементарными исходами этого опыта и образуют пространство элементарных исходов, обозначаемое Ω. Элементарные исходы взаимно исключают друг друга и составляют полную группу событий.

Опыт составляет схему случаев, если все его элементарные исходы равновозможны и их число конечно.

Испытание – осуществление каждого отдельного наблюдения, опыта или измерения.

Любой факт, который может наступить в результате испытания, называется событием.

Если событие обязательно наступит при данном комплексе условий, то его называют достоверным и обозначают U. Если событие никогда не наступит при данном комплексе условий, то его называют невозможным и обозначают V.

События, которые в результате испытания могут произойти или не произойти, называются случайными. Любое случайное событие есть подмножество пространства Ω, соответствующее данному опыту.

Событие называется простым, если его невозможно разложить на составляющие и сложным (составным), если такое разложение возможно.

Сложное событие может представлять логическую сумму или логическое произведение нескольких событий.

Логическая сумма – наступление хотя бы одного из нескольких событий. Например,

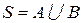– сумма двух событий;

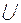– символ логического сложения.

Логическое произведение – совместное наступление нескольких событий одновременно или последовательно друг за другом. Например, 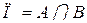– произведение двух событий;

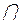– символ логического произведения.

Элементарный исход опыта называется благоприятствующим данному событию, если его осуществление влечет за собой наступление этого события.

Каждое событие обладает объективной возможностью наступления.

Численная мера объективной возможности наступления называется вероятностью события. Вероятность – главная характеристика случайного события.

Если опыт сводится к схеме случаев, то вероятность вычисляют по формуле

,

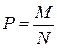где N - число всех равновозможных исходов опыта, а M – число тех из них, которые благоприятствуют наблюдаемому событию. Это – классическое определение вероятности, введенное Лапласом.

Если опыт невозможно свести к схеме случаев, то проводят испытания, и вероятность оценивают по приближенной формуле

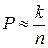
где n – число испытаний, а k – число наступлений события в этих испытаниях. Это – статистическое определение вероятности события.

Для подсчета числа равновозможных исходов опыта часто используют формулы комбинаторики: перестановки, размещения и сочетания.

Перестановки множества – упорядоченные множества, полученные из того же множества, которые отличаются лишь порядком следования элементов.

Число перестановок равно .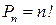

Размещения множества из n элементов по k отличаются либо самими элементами, либо порядком их следования.

Число размещений из n элементов по k равно .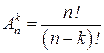

Сочетания из n элементов по k отличаются хотя бы одним элементом.

Число сочетаний из n элементов по k равно .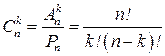

Например, для множества из 3-х различимых элементов: a, b, c:

1. Перестановки множества: abc, acb, bac, bca, cab, cba.

Их число равно.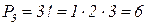

2. Размещения из 3-х элементов группами по 2: ab, ac, ba, bc, ca, cb.

Их число равно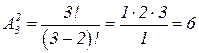

3. Сочетания из 3-х элементов по 2: ab, ac,bc.

Их число равно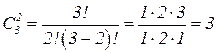

Формулы классического и статистического определения вероятности выражают прямые способы вычисления вероятностей случайных событий. Они являются центральными, но не основными. Основными следует считать к освенные способы, позволяющие по известным событиям одних событий вычислять вероятности других, логически с ними связанных.