2015-04-23
443
Нормальный закон распределения описывает распределение непрерывной СВ и наиболее часто встречается на практике. Ему подчиняются, например, случайные ошибки измерений и сами результаты измерений. Нормальное распределение принято за эталон.
Если НСВ X подчиняется нормальному закону распределения, то это записывают так: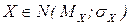 
, где MX и σX – параметры распределения. Так случайные ошибки измерений 
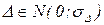, т.е. математическое ожидание M ∆ случайной ошибки равно нулю.
Плотность вероятности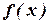 
нормального распределения:
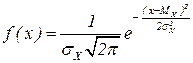
Функция F(x) нормального распределения:
.
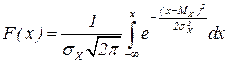После замены переменных и введения переменно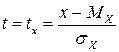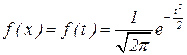й 
и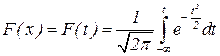 
.
Для вычисления вероятности попадания нормально распределенной СВ в заданный интервал [ α, β) применяется формула
,
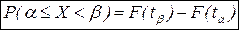где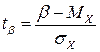 
и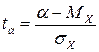 
.
Если аргумент t отрицательный, то F(– t) = 1 – F(t).
Значения функций F(t) и f(t) приведены в соответствующих таблицах, а также могут быть получены на компьютере (EXEL, MathCad и т.п.).
Для вычисления вероятности попадания СВ X, имеющей MX = 0, т.е. нулевое математическое ожидание (например, случайная ошибка измерений) в интервал с симметричными границами удобнее использовать функцию Лапласа (интеграл вероятностей) Ф(t):
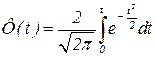или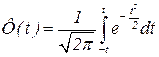 
,
где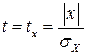 
, т.к. MX = 0. Тогда 
.
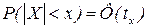Таблица значений функции Лапласа
| t | Ф(t) | t | Ф(t) |
| 0 | 0 | 2.0 | 0.955 |
| 0.5 | 0.383 | 2.5 | 0.988 |
| 1.0 | 0.683 | 3.0 | 0.997 |
| 1.5 | 0.866 | 3.5 | 1.000 |
Биномиальный закон распределения описывает распределение дискретной СВ
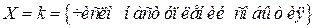
в n испытаниях Бернулли.
В этих испытаниях возможные значения ДСВ X = k: 0, 1, 2,…,n, а вероятности этих значений вычисляются по формуле Бернулли.
Ряд распределения для биномиального закона имеет вид:
| X = k | 0 | 1 | 2 | … |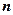 
|
| Pk(n) | P0(n) | P1(n) | P2(n) | … | Pn(n) |
. При этом всегда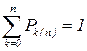 
Основные числовые характеристики биномиального распределения можно получить по простым формулам:
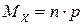– мат. ожидание;
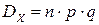– дисперсия;
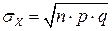– ср. кв. отклонение.
При большом числе испытаний n вычисление вероятностей Pk(n) по формуле Бернулли имеет малое практическое значение. Чаще возникает задача определения вероятности Р(α≤X≤β)(n) попадания ДСВ на заданный интервал ее значений, которая решается согласно теореме Муавра-Лапласа. В ней утверждается, что предельным случаем биномиального распределения, когда n →∞, причем ни одна из величин p и q не очень мала, – является нормальное распределение. Тогда
,
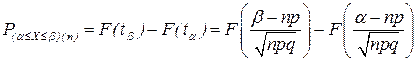где F(t) – функция нормального распределения.
