2015-04-23
1337
В дифференциальном исчислении по заданной функции 
приходилось отыскивать ее производную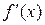 
.
В интегральном исчислении рассматривается обратная задача: по заданной функции восстановить такую функцию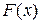 
, для которой была бы производной, т.е.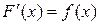 
.
Определение. Функция 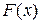называется первообразной (функцией) для функции на интервале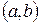 
, если для всех значений x из этого интервала выполняется равенство
.
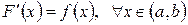Примеры
1) Функция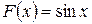 
является первообразной для функции 
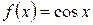на всей числовой прямой, так как при любом значении 
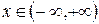выполняется равенство 
.
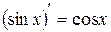2) Функция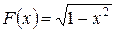 
является первообразной для функции 
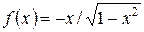на интервале 
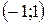, так как в любой точке x этого интервала 
.
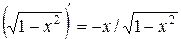Однако задача отыскания по данной функции её первообразной решается неоднозначно. Действительно, если 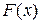– первообразная для , т.е. 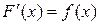, то функция 
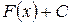, где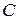 
– произвольная постоянная, также является первообразной для , так как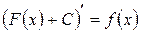 
для любого числа .
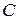Например, для 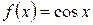первообразной является не только 
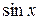, но и функция 
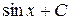, так как 
.
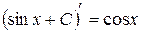Возникает вопрос: если 
и 
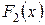– две первообразные для одной и той же функции , то всегда ли они отличаются друг от друга на постоянное слагаемое? Оказывается, что это действительно так.
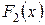Теорема 1.1. Если и – две первообразные для функции на интервале 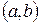, то 
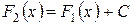, где 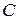– некоторая постоянная.
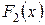Доказательство. По условию и – первообразные для , поэтому
.
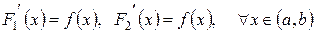Рассмотрим функцию
.
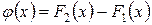Её производная
.
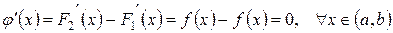Для любых двух точек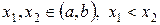 
по теореме Лагранжа получаем
.
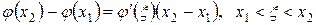Так как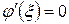 
, то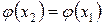 
. Это означает, что значения функции 
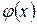во всех точках интервала 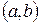одинаковы, т.е. 
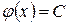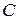, где – некоторое число. Таким образом, 
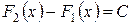или .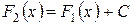
Следствие. Все первообразные для функции на интервале 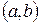даются формулой 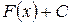, где 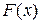– одна из первообразных для , а 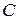– произвольная постоянная.
