1) Интегралы вида: 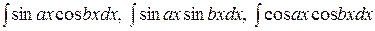 .
.
Чтобы вычислить эти интегралы, следует представить подынтегральное произведение в виде суммы, используя формулы:
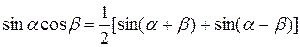 ,
,
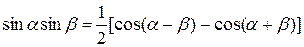 ,
,
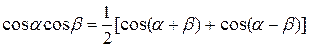 .
.
Пример 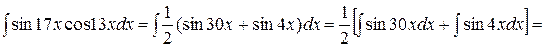
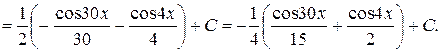
2) Интегралы вида: 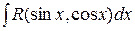 ,
,
где R – рациональная функция от тригонометрических аргументов 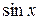 и
и 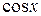 .
.
Такие интегралы сводятся к интегралам от рациональных функций от «обычных» аргументов с помощью соответствующих, в зависимости от вида функции 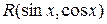 , подстановок:
, подстановок:
а) 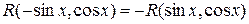 – нечетная функция от
– нечетная функция от 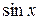 .
.
Подстановка 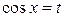 .
.
б) 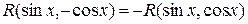 – нечетная функция от
– нечетная функция от 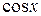 .
.
Подстановка 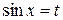 .
.
в) 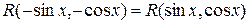 – четная функция от
– четная функция от 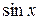 и
и 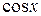 .
.
Подстановка 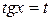 .
.
г) 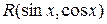 – произвольная рациональная функция от
– произвольная рациональная функция от 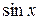 и
и 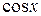 .
.
Подстановка 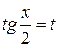 (универсальная).
(универсальная).
Пример
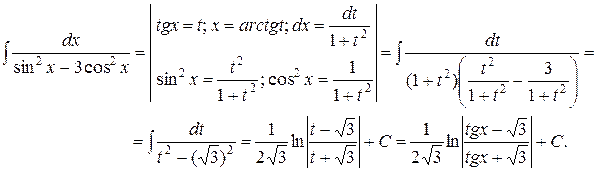
 2015-04-23
2015-04-23 2333
2333
