1. Непосредственное интегрирование. Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием или методом разложения.
Пример
 .
.
2. Метод подстановки (замены переменной). Метод, позволяющий с помощью введения новой переменной интегрирования свести нахождение данного интеграла к нахождению табличного интеграла, называется методом подстановки или методом замены переменной.
Метод основан на следующей теореме.
Теорема 1.3. Пусть функция 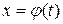 определена и дифференцируема на некотором множестве T и пусть X – множество значений этой функции, на котором определена функция
определена и дифференцируема на некотором множестве T и пусть X – множество значений этой функции, на котором определена функция 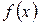 . Тогда, если на множестве X функция
. Тогда, если на множестве X функция 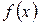 имеет первообразную, то на множестве T справедлива формула замены переменной в неопределенном интеграле:
имеет первообразную, то на множестве T справедлива формула замены переменной в неопределенном интеграле:
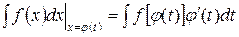 .
.
Доказательство. Пусть 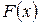 – первообразная для
– первообразная для 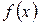 на множестве X. Рассмотрим на множестве T сложную функцию
на множестве X. Рассмотрим на множестве T сложную функцию 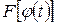 . По правилу дифференцирования сложной функции, учитывая, что
. По правилу дифференцирования сложной функции, учитывая, что 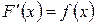 , получаем
, получаем
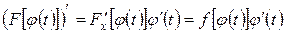 ,
,
т.е. функция 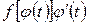 имеет на множестве T первообразную
имеет на множестве T первообразную 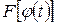 и, следовательно,
и, следовательно,
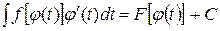 .
.
Но
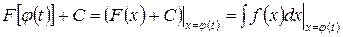 ,
,
поэтому
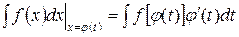 .
.
Пример
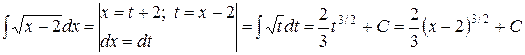 .
.
Иногда формулу замены переменной полезно применять справа налево:
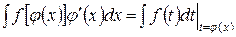 .
.
Пример
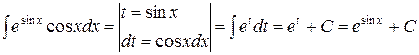 .
.
3. Метод интегрирования по частям. Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.
Теорема 1.4. Пусть функции 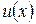 и
и 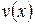 определены и дифференцируемы на некотором промежутке X и пусть функция
определены и дифференцируемы на некотором промежутке X и пусть функция 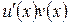 имеет первообразную на этом промежутке. Тогда на промежутке X функция
имеет первообразную на этом промежутке. Тогда на промежутке X функция 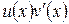 также имеет первообразную и справедлива формула интегрирования по частям в неопределенном интеграле:
также имеет первообразную и справедлива формула интегрирования по частям в неопределенном интеграле:
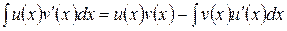 .
.
Доказательство. Из равенства
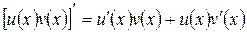
получаем
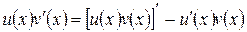 .
.
Первообразной функции 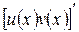 на промежутке X является функция
на промежутке X является функция 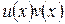 . Функция
. Функция 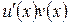 имеет первообразную на X по условию теоремы. Следовательно, и функция
имеет первообразную на X по условию теоремы. Следовательно, и функция 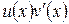 имеет первообразную на промежутке X. Интегрируя последнее равенство, получаем формулу интегрирования по частям.
имеет первообразную на промежутке X. Интегрируя последнее равенство, получаем формулу интегрирования по частям.
Замечание. Так как 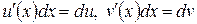 , то формулу интегрирования по частям в неопределенном интеграле можно записать в виде
, то формулу интегрирования по частям в неопределенном интеграле можно записать в виде
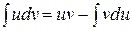 .
.
Пример
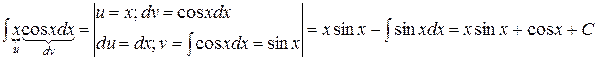 .
.
Замечание. Формула интегрирования по частям может применяться неоднократно.
Пример
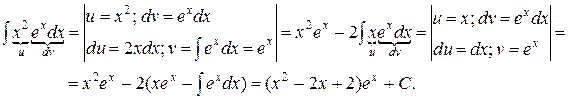
 2015-04-23
2015-04-23 774
774








