Неопределенный интеграл. Определение. Совокупность всех первообразных для функции на интервале 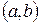называется неопределенным интегралом от функции на этом интервале и обозначае

Определение. Совокупность всех первообразных для функции на интервале называется неопределенным интегралом от функции на этом интервале и обозначается символом

.

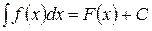При этом функция называется подынтегральной функцией, 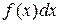– подынтегральным выражением, а переменная x – переменной интегрирования.

Нахождение первообразных для функции называется интегрированием функции .

Отметим, что подынтегральное выражение является дифференциалом первообразной:

.

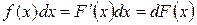Примеры

1) 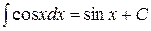, так как .

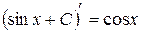2) 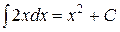, так как .

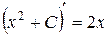Теорема 1.2. Если функция непрерывна на интервале 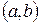, то для неё существует первообразная на 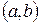, а следовательно, и неопределенный интеграл.

Доказательство этой теоремы будет дано позже (см. теорему 2.2).