2015-04-23
2780
Важный класс функций, интегралы от которых всегда выражаются через элементарные функции, образуют элементарные функции.
Определение. Функция
,
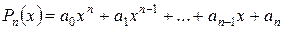где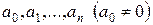 
– заданные числа (коэффициенты), называется многочленом или полиномом или целой рациональной функцией степени n.
Отношение двух многочленов
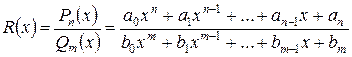
называется рациональной функцией или рациональной дробью. Рациональная дробь будет правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе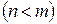 
, и неправильной в противном случае 
.
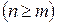Рассмотрим, как вычисляются интегралы 
от рациональных дробей.
Если дробь
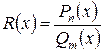
неправильная, то следует разделить (как обычно, столбиком) числитель на знаменатель. Частное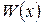 
и остаток 
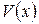будут многочленами, причем степень остатка 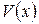меньше степени делителя 
:
.
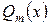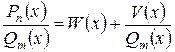Пример
; 
.
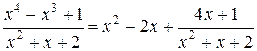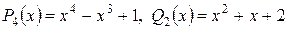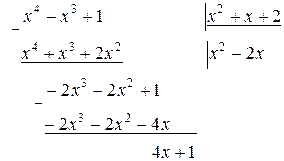
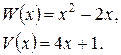
Дробь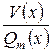 
– правильная, а интеграл 
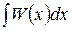от многочлена 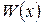легко берется методом непосредственного интегрирования.
Таким образом, интегрирование неправильной дроби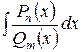 
свелось по сути к интегрированию правильной дроби 
:
.
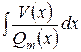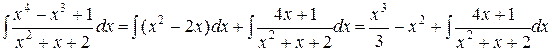Поэтому достаточно научиться интегрировать правильные дроби.
Известно (см., например, ч.1, раздел 5.3), что многочлен 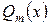с действительными коэффициентами может быть разложен на линейные и квадратичные действительные множители:
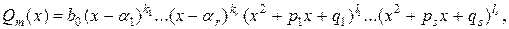
где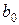 
– старший коэффициент многочлена. Каждый линейный множитель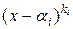 
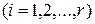соответствует действительному корню 
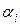кратности 
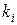, а каждый квадратичный множитель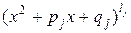 
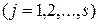соответствует паре комплексно-сопряженных корней 
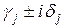кратности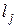 
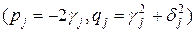, причем 
.
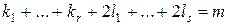В высшей алгебре доказывается, что всякая правильная дробь может быть единственным образом разложена на сумму так называемых простейших дробей:
,
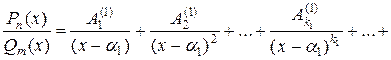
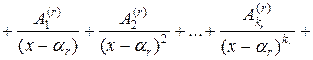
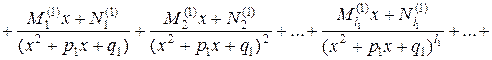
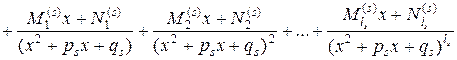где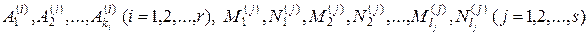 
– некоторые действительные числа – коэффициенты разложения. Для их определения умножим обе части разложения на 
и приравняем коэффициенты, стоящие при равных степенях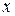 
, у многочлена, который получится в правой части разложения и многочлена 
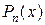. В результате получим систему линейных алгебраических уравнений, из которой и найдем неизвестные коэффициенты разложения. Такой метод отыскания коэффициентов разложения правильной рациональной дроби на простейшие дроби называется методом неопределенных коэффициентов.
Пример. Разложить правильную рациональную дробь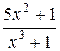 
на простейшие дроби.
Так как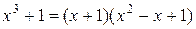 
, то разложение имеет вид
.
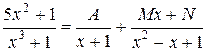Умножая обе части равенства на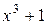 
, получаем
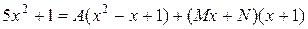
или
.
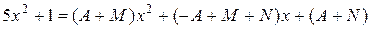Приравнивая коэффициенты при одинаковых степенях 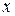, получаем систему линейных алгебраических уравнений относительно неизвестных коэффициентов разложения 
:
.
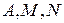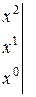
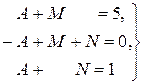Решение системы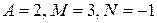 
, поэтому искомое разложение имеет вид:
.
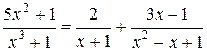Замечание. Систему линейных уравнений для определения неизвестных коэффициентов разложения можно также получить, придавая последовательно столько различных произвольных значений, сколько имеется неизвестных коэффициентов (в данном примере – три):
,
.
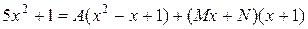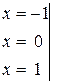
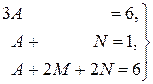
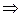
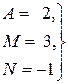Из изложенного следует, что задача интегрирования правильной рациональной дроби сводится, в свою очередь, к нахождению интегралов от простейших дробей следующих четырех типов:
I) 
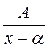; II)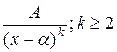 
;
III)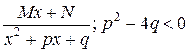 
; IV)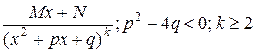 
.
Дроби I и II типов элементарно интегрируются при помощи подстановки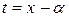 
:
I)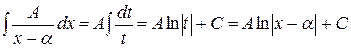 
.
II)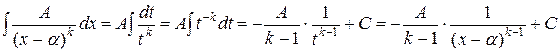 
.
Для вычисления интеграла от дроби III типа представим квадратный трехчлен в виде
.
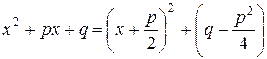Учитывая, что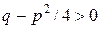 
, введем в рассмотрение действительную постоянную 
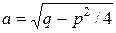. Сделав подстановку 
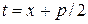, будем иметь:
=
= 
=
= 
=
= 
.
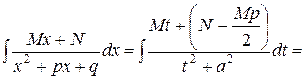
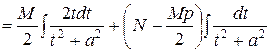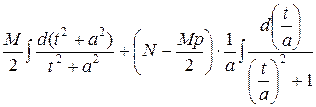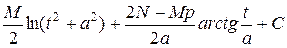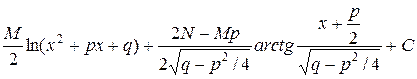Пример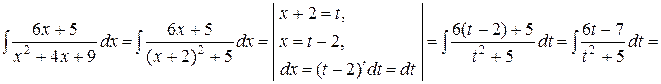 
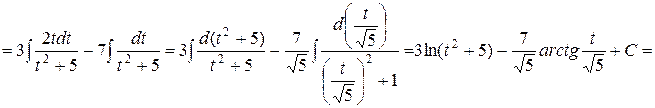
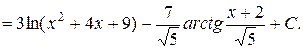
Остается вычислить интеграл от дроби IV типа.
Используя введенные выше обозначения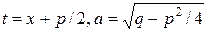 
, будем иметь:
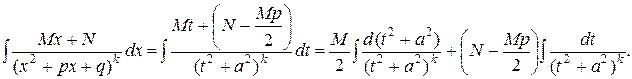
Введем обозначения:
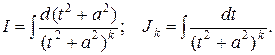
Интересующий нас интеграл будет найден, если будут найдены интегралы I и Jk:
.
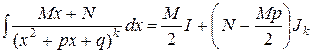Интеграл I берется элементарно:
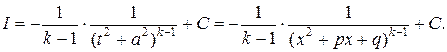
Для вычисления интеграла Jk установим для него рекуррентную (возвратную) формулу, сводящую вопрос о вычислении Jk к вычислению Jk-1.
Можно записать (при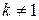 
):
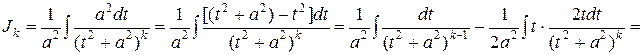
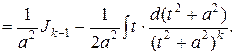
Для вычисления последнего интеграла применим формулу интегрирования по частям:
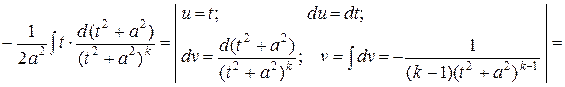
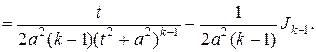
Находим
.
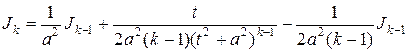Из последнего равенства получаем рекуррентную формулу
,
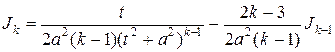по которой интеграл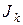 
можно выразить через интеграл 
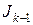, затем 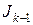, в свою очередь, выразить через 
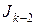и т.д. Процесс вычисления 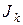продолжаем до тех пор, пока не дойдем до
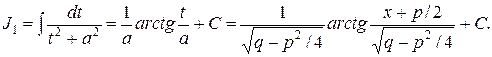
Итак, нами вычислены интегралы от всех четырех простейших дробей. Установлено, что интегрирование любой рациональной функции сводится к интегрированию многочлена и конечного числа простейших дробей, интегралы от которых выражаются через рациональные функции, логарифмы и арктангенсы. Иными словами, любая рациональная функция интегрируется в элементарных функциях.
