Основные свойства неопределенного интеграла

Свойство 1. Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению:

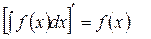и .

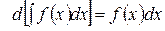Доказательство.

;

.

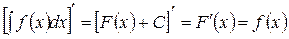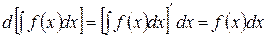Свойство 2. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:

.

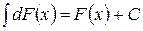Доказательство.

.

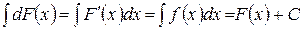Свойство 3. Постоянный множитель можно выносить за знак интеграла:

.

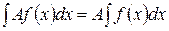Доказательство. Прежде всего подчеркнем, что данное равенство имеет условный характер: его следует понимать как равенство правой и левой частей с точностью до произвольного постоянного слагаемого, поскольку каждый из интегралов определен с точностью до произвольного постоянного слагаемого.

Действительно, пусть 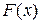– первообразная для функции , т.е. 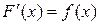. Тогда 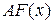– первообразная для функции 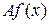, так как 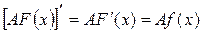. Отсюда следует, что

,

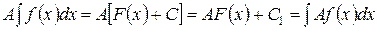где 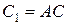– произвольная постоянная.

Свойство 4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от этих функций:

.

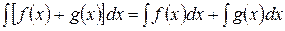Доказательство. Данное равенство (как и в предыдущем свойстве) следует понимать как равенство правой и левой частей с точностью до произвольного постоянного слагаемого, поскольку каждый из интегралов определен с точностью до произвольного постоянного слагаемого.

Действительно, пусть 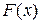и 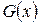– первообразные для функций и 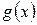соответственно, т.е. 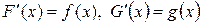. Тогда функция 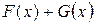является первообразной для функции 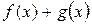, так как

.

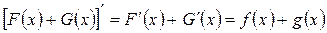Следовательно,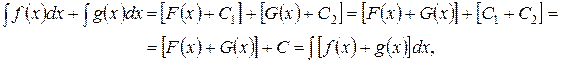

где 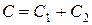– произвольная постоянная.

Отметим, что данное свойство справедливо для любого конечного числа слагаемых функций.

Таблица основных интегралов

Приведем таблицу основных интегралов, которая непосредственно следует из определения интегрирования как операции, обратной дифференцированию, и таблицы производных. Справедливость всех формул легко проверить дифференцированием первообразных. Интегралы, содержащиеся в этой (или подобной ей) таблице, принято называть табличными.

Таблица интегралов в силу инвариантности формы дифференциала функции оказывается справедливой независимо от того, является ли переменная интегрирования 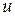независимой переменной 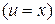или любой её дифференцируемой функцией ().

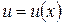1. .

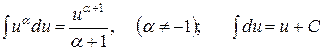2. .

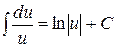3. .

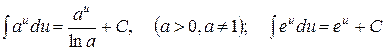4. .

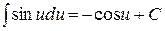5. .

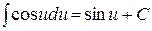6. .

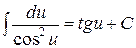7. .

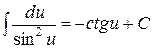8. .

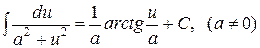9. .

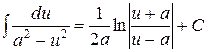10. .

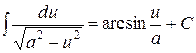11. .

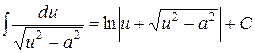12. .

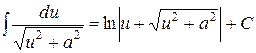13. .

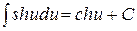14. .

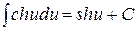15. .

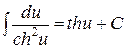16. .

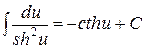Отметим, что если операция дифференцирования элементарных функций снова приводит к элементарным функциям, то операция интегрирования уже может привести к неэлементарным функциям, т.е. функциям, которые не выражаются через конечное число арифметических операций и суперпозиций элементарных функций.

Например, доказано, что следующие интегралы хотя и существуют, но не являются элементарными функциями:

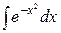– интеграл Пуассона;

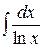– интегральный логарифм;

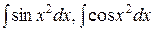– интегралы Френеля.